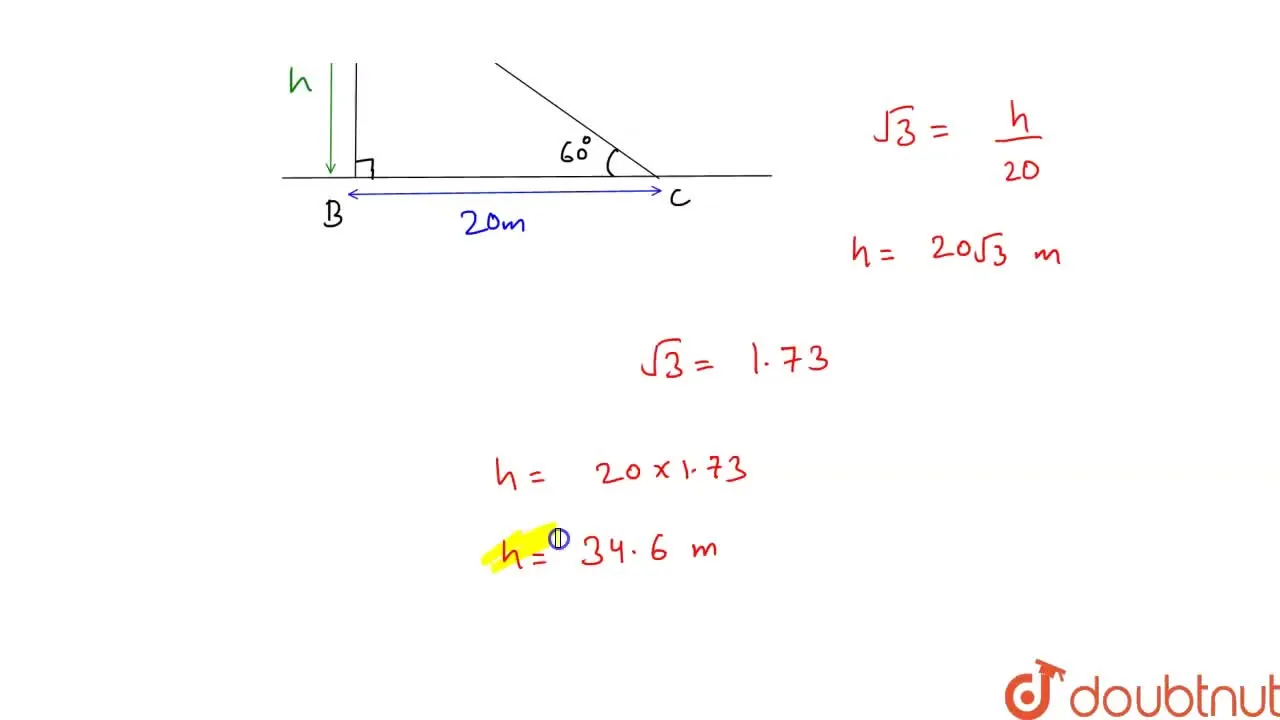
From a point on the ground 20 m away from the foot of a tower the angle of elevation is 60∘. What is the height of tower?
Step by step video & image solution for From a point on the ground 20 m away from the foot of a tower the angle of elevation is 60^(@). What is the height of tower? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - PRACTICE-TEST (SECTION-C)2videos
SOME APPLICATIONS OF TRIGONOMETRY
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - PRACTICE-TEST (SECTION-D)1videos
SOME APPLICATIONS OF TRIGONOMETRY
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - PRACTICE-TEST (SECTION-A)4videos
SOME APPLICATIONS OF TRIGONOMETRY
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - REAL NUMBERSEXERCISE - LONG ANSWER TYPE QUESTION15videos
REAL NUMBERS
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - Practice -Test5videos
STATISTICS
Similar Questions
From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘. The angle of elevation of the top of a water tank(on the top of tower) is 45∘.find the height of the tower and depth of tank
View SolutionA tower stands vertically on the ground. From a point on the ground which is 30 m away from the foot of a tower, the angle of elevation of the top of the tower is found to be 45∘. Find the height of the tower.
View SolutionFrom a point on the ground, 20m away from the foot of a vertical tower, the angle of elevation of the top of the tower is 60o , what is the length of the tower?
View SolutionFrom a point on the ground 40m away from the foot of a tower, the angle of elevation of the top of the tower is 30o . The angle of elevation of the top of a water tank (on the top of the tower) is 45o . Find the (i) height of the tower (ii) the depth of the tank.
View SolutionA tower stands vertically on the ground. From a point on the ground, 20m away from the foot of the tower, the angle of elevation of the top of the tower is 60o . What is the height of the tower?
View SolutionFrom a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ . The height of the tower is
View SolutionFrom 40 m away from the foot of a tower , the angle of elevation of the top of the tower is 60∘ .What is the height of the tower ?
View SolutionA tower stands vertically on the ground. From a point on the ground, which is 15m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 60∘. Find the height of the tower.
View SolutionAt a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ The height of the tower is
View SolutionA tower stands vertically on the ground. From a point on the ground, which is 15 m away from the foot of the tower is found to be 60∘. Find the height of the tower.
View Solution