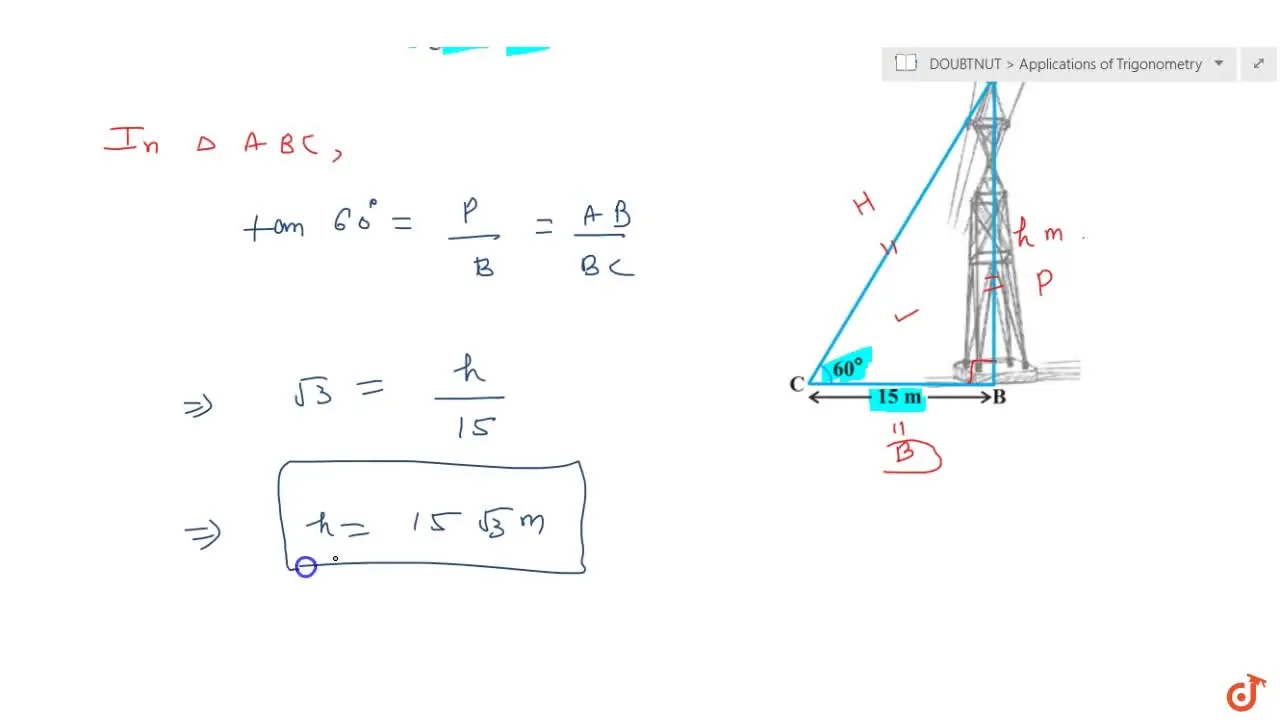
A tower stands vertically on the ground. From a point on the ground, which is away from the foot of the tower, the angle of elevation of the top of the tower is found to be . Find the height of the tower.
None
The correct Answer is:B
From the given data,
also,
= height of tower / distance of point from foot of tower
The calculated of height of tower is
Related Playlists
Similar Questions
A tower stands vertically on the ground. From a point on the ground which is 30 m away from the foot of a tower, the angle of elevation of the top of the tower is found to be 45∘. Find the height of the tower.
View SolutionFrom a point on the ground which is at a distance of 50 m from the foot of the towe, the angle of elevation of the top of the tower is observed to be 30∘. Find the height of the tower.
View SolutionA tower stands vertically on the ground. From a point on the ground, which is 15 m away from the foot of the tower is found to be 60∘. Find the height of the tower.
View Solution80 m away from the foot of the tower, the angle of elevation of the top of the tower is 60∘. What is the height (in metres) of the tower?
View SolutionFrom 40 m away from the foot of a tower , the angle of elevation of the top of the tower is 60∘ .What is the height of the tower ?
View SolutionA tower stands vertically on the ground. From a point on the ground, 20m away from the foot of the tower, the angle of elevation of the top of the tower is 60o . What is the height of the tower?
View SolutionFrom a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ . The height of the tower is
View SolutionAt a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ The height of the tower is
View SolutionFrom a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘. The angle of elevation of the top of a water tank(on the top of tower) is 45∘.find the height of the tower and depth of tank
View SolutionAt a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ The height of the tower is
View Solution