ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD . Show that(i) ΔAPB≅ ΔCQD(ii) AP = CQ
The correct Answer is:Prove
Step by step video, text & image solution for ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD . Show that(i) DeltaA P B~=\ DeltaC Q D(ii) A P\ =\ C Q by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUARILATERAL BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - QUARILATERAL EXERCISE - Part - D
5 Videos
- QUARILATERAL BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - QUARILATERAL EXERCISE - Part - B
12 Videos
- PROBABILITY MIND MAPBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROBABILITY MIND MAPEXERCISE - PRACTICE TEST
6 Videos
- STATISTICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - PRACTICE TEST
5 Videos
Similar Questions
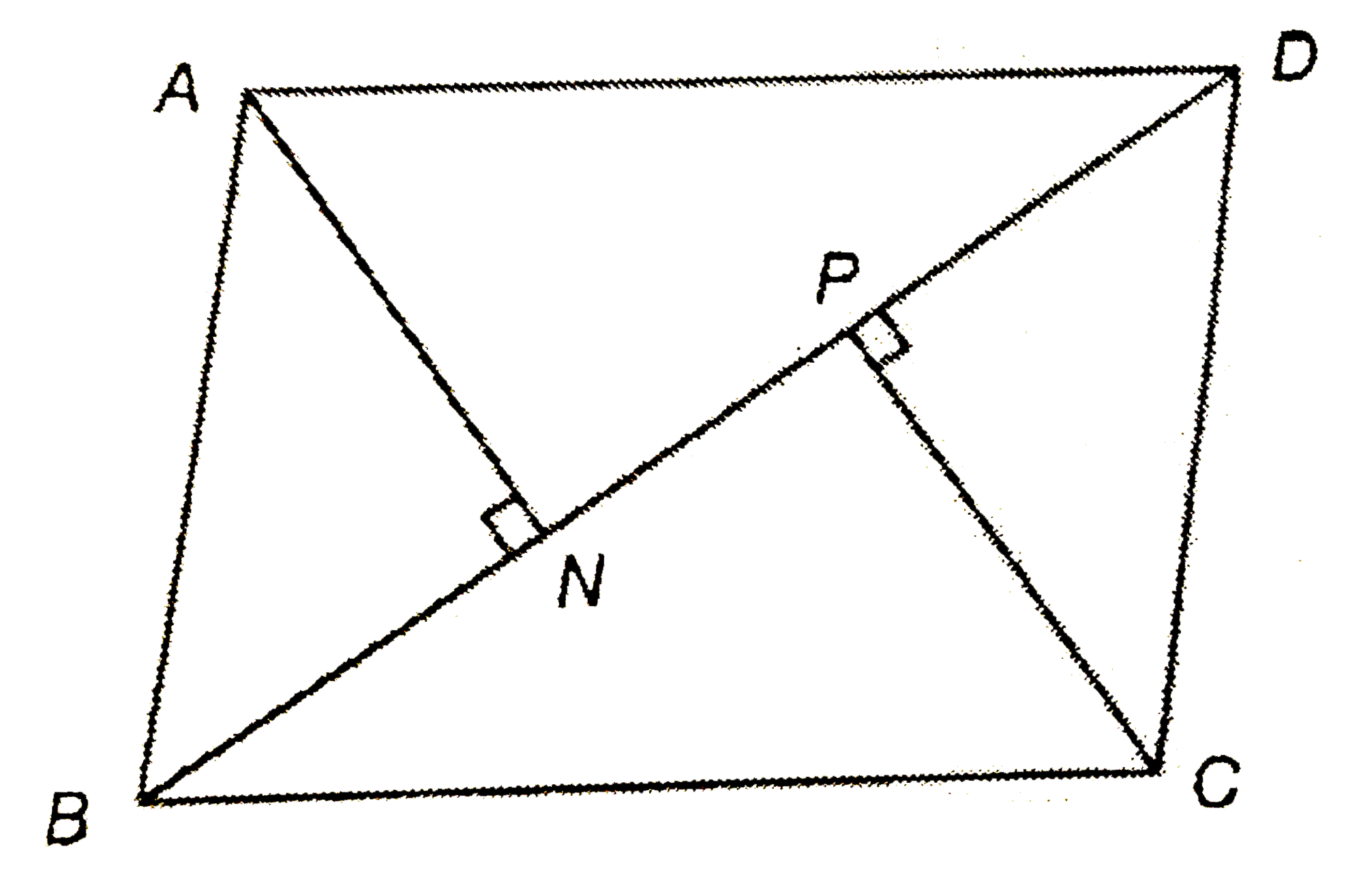
In the given figure, ABCD is a parallelogram in which AN and CP are perpendiculars on diagonal BD. Prove that :
(i) ΔADN=ΔCBP
(ii)AN=CP
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that:
(i) ΔAPD≅ΔCQB
(ii) AP=CQ
(iii) ΔABC
(iv) AQ=CP
(v) APCQ is a parallelogram.

View Solution
Knowledge Check
ABCD is a parallelogram. P and Q are mid points of BC & CD. Find the area of ΔAPQ if area of ΔABC is 12.
AtrapeziumBparallelogramCsquareDnone of theseABCD is a parallelogram with AC and BD as diagonals. Then, A→C−B→D=
A4A→BB3A→BC2A→BDA→BABCD is a parallelogram, P and Q are the points on the diagonal AC such that AP=QC, then quadrilateral BPDQ is a :
AtrapeziumBparallelogramCsquareDnone of these
line l is the bisector of an angle ∠A and∠Bis any point on l. BP and BQ are perpendiculars from B to the arms of ∠A. Show that:
(i) ΔAPB≅ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A

View SolutionIn a parallelogram ABCD, points P and Q are points of trisection of diagonal BD. Prove that CQ is parallel to AP.
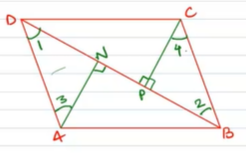
View SolutionIn Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that : ADN≅CBP (ii) AN=CP
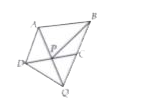
View SolutionIn the figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar(ΔBPC) = ar(ΔDPQ).
View SolutionABCD is a parallelogram. ¯¯¯¯¯¯AP bisects ∠Aand¯¯¯¯¯¯CQ bisects ∠C.P lies on ¯¯¯¯¯¯CDandQ lies on ¯¯¯¯¯¯¯¯AB0. Show that -
View Solution
