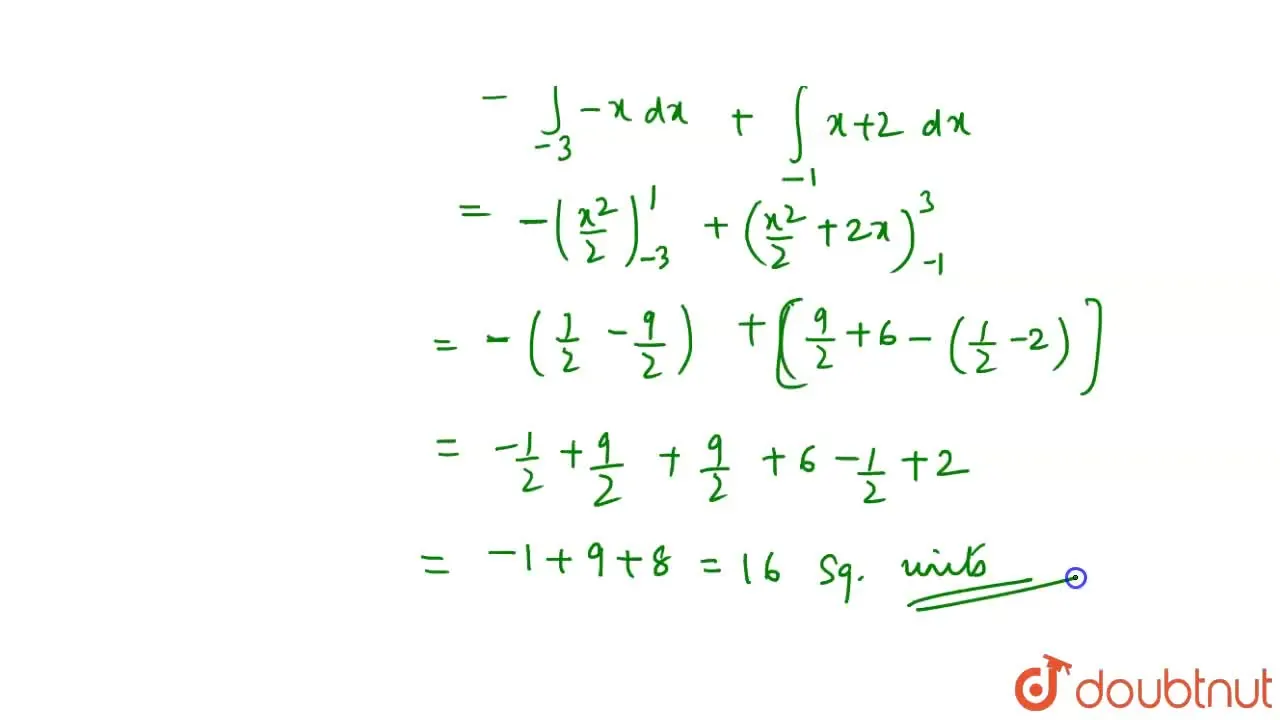Using integration, find the area of the region bounded by the curve y=1+|x+1| and lines x=−3,x=3,y=0.
The correct Answer is:16 sq. units
Step by step video, text & image solution for Using integration, find the area of the region bounded by the curve y= 1+|x+1| and lines x =-3, x = 3, y=0. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
Using integration, find the area of the region bounded by the curve y2=9x and lines x=1 and x=4.
View SolutionThe area of the region bounded by the curve y=x+1 and the lines x=2,x=3, is
View SolutionThe area of the region bounded by the curve y = x + 1 and the lines x=2,x=3, is
View SolutionUsing integration, find the area of the region bounded by the parabola y2=16x and the line x=4
View SolutionFind the area of the region bounded by the curve y2=4x and the line x=3.
View SolutionUsing intergration, find the area of the region bounded by the curve y2=x,x=1,x=4 and X-axis.
View SolutionFind the area of the region bounded by the curve xy=1 and the lines y=x,y=0,x=e
View SolutionUsing integration, find the area of the region bounded by the lines Y=1+|x+1|,x=−2,x=3andy=0.
View SolutionUsing integration, find the area of the region bounded by the parabola y2=4x and the line x=4.
View SolutionFind the area of the region bounded by the curve y=|x+1|, lines x=−4,x=2 and X-axis.
View Solution