One end of each of two identical springs, each of force constant 0.5N/m are attached on the opposite sides the a wooden block of mass 0.01kg. The other ends of the spring are connected to separate rigid supports such that the springs are unstrtched and are collinear in a horizontal plane. To the wooden piece is fixed a pointer which touches a vertically moving plane paper. The wooden piece kept on a smooth horizontal table is now displaced by 0.02m along the line of springs and released. If the speed of paper is 0.1m/s, find the equation of the path traced by the pointer on the paper and the distance between two consecutive maximum on this path.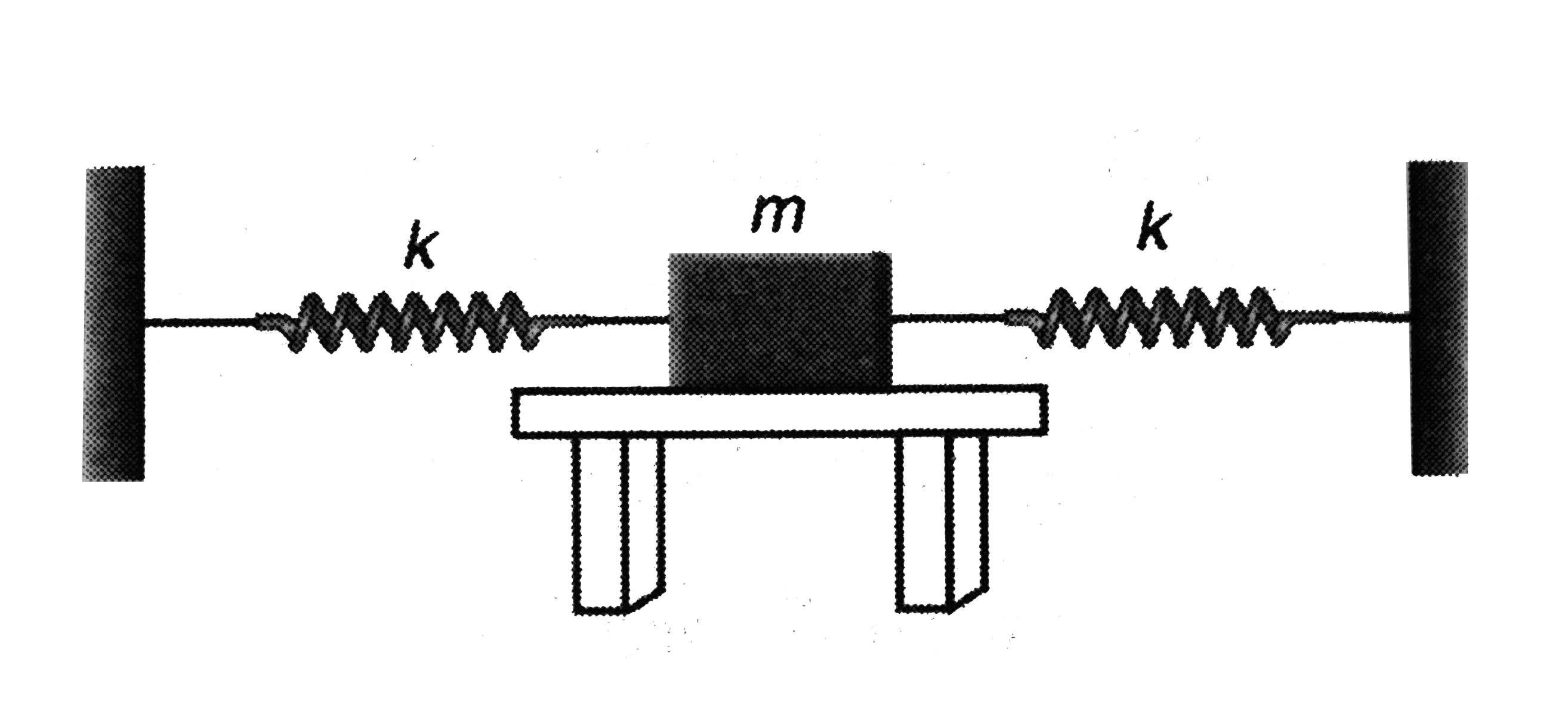 
The correct Answer is:A, B
Step by step video, text & image solution for One end of each of two identical springs, each of force constant 0.5N//m are attached on the opposite sides the a wooden block of mass 0.01kg. The other ends of the spring are connected to separate rigid supports such that the springs are unstrtched and are collinear in a horizontal plane. To the wooden piece is fixed a pointer which touches a vertically moving plane paper. The wooden piece kept on a smooth horizontal table is now displaced by 0.02m along the line of springs and released. If the speed of paper is 0.1m//s, find the equation of the path traced by the pointer on the paper and the distance between two consecutive maximum on this path. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Advance MCQs with One or More Options Correct30videos
WAVES
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems28videos
WAVE OPTICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - X-RAYSEXERCISE - Unsolved Numerica Problem for Preparation23videos
X-RAYS
Similar Questions
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.
View Solution
Knowledge Check
- Question 1 - Select One
A spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is
Av√(mk)Bmv√kCm√(vk)Dk√(mv) - Question 2 - Select One or More
A spring with one end attached to a mass and the other to a right support is stretched and released
AMagnitude of acceleration when just releases is maximumBMagnitude of acceleration, when at equilibrium position is maximumCspeed is maximum when mass is a equilibrium position.DMagnitude of displacement is always maximum whenever speed is minimum - Question 3 - Select One
On a smooth inclined plane a body of mass M is attached between two springs. The other ends of the spring are fixed to ffirm supports. If each spring has a force constant k, the period of oscillation of the body is: (assuming the spring as massless)
A2π√M2KB2π√2MKC2π√MSinθKD2π√2MSinθK
An ideal spring of force constant k is broken into two identical pieces. The force constant of each of the smaller springs is :
View SolutionAn ideal spring of force constant k is broken into two identical pieces. The force constant of each of the smaller springs is :
View SolutionTwo springs of spring constant 6N/m and 4N/m are attached to a block of mass 1 kg and to fixed support. Then time period of the given oscillation is
(consider √10=π)View SolutionOn a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)
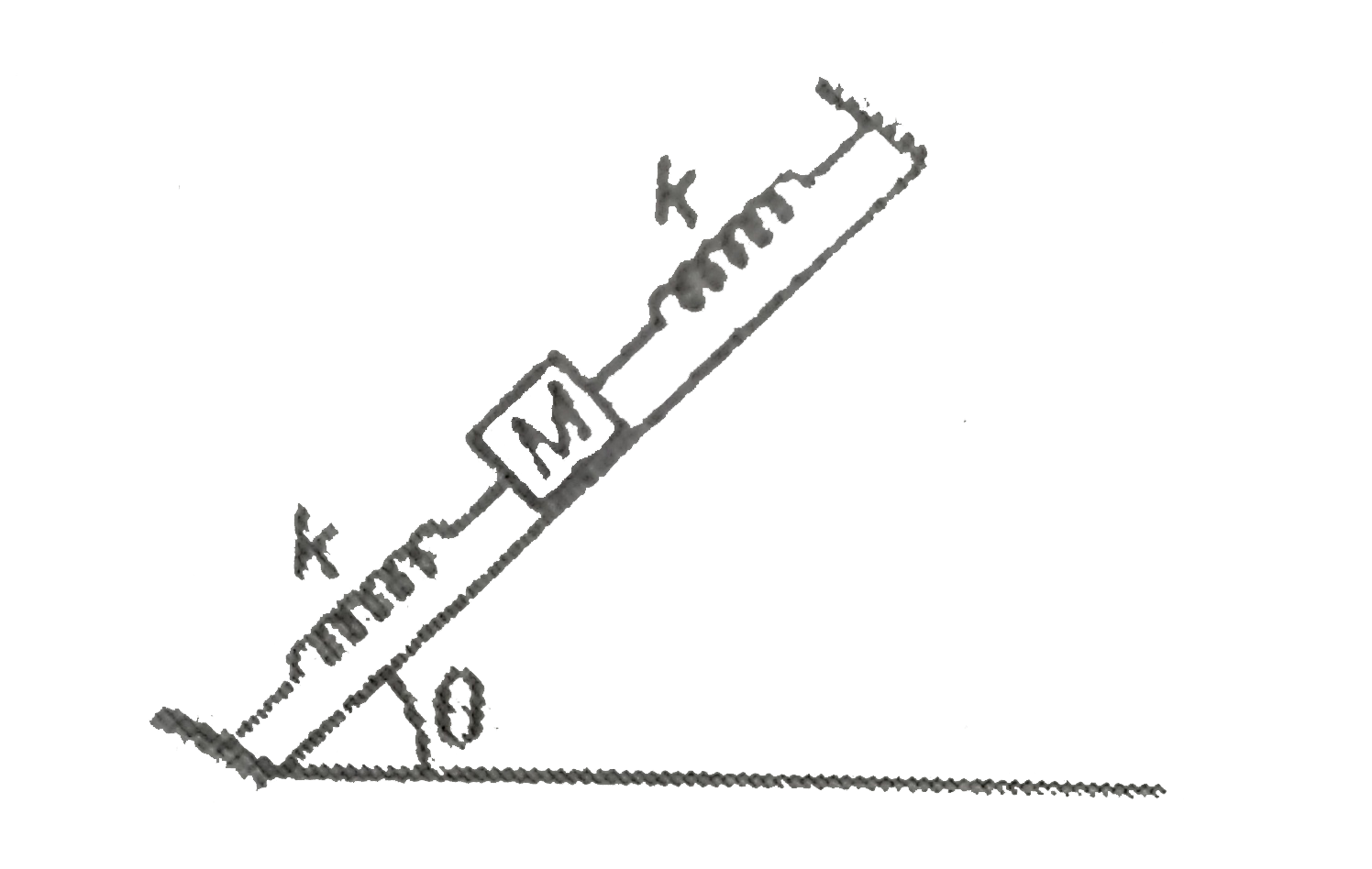
View SolutionOn a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is
View Solution