In a good FM radio receiver, the radio signal detected may be as much as 65 dB greater than the noise signal. What is the ratio of signal intensity to noise intensity ?
The correct Answer is:3.16×106
To find the ratio of signal intensity to noise intensity given that the radio signal is 65 dB greater than the noise signal, we can follow these steps:
1. Understand the Decibel Formula:
The loudness in decibels (dB) is given by the formula:
L=10log10(II0)
where I is the intensity of the signal and I0 is a reference intensity (usually 10−12W/m2).
2. Set Up the Loudness Equations:
Let IR be the intensity of the radio signal and IN be the intensity of the noise signal. The loudness of the radio signal (LR) and the noise signal (LN) can be expressed as:
LR=10log10(IRI0)
LN=10log10(INI0)
3. Use the Given Information:
According to the problem, the difference in loudness is given as:
LR−LN=65dB
4. Substitute the Loudness Equations:
Substitute the expressions for LR and LN into the equation:
10log10(IRI0)−10log10(INI0)=65
5. Factor Out the 10:
Dividing the entire equation by 10 gives:
log10(IRI0)−log10(INI0)=6.5
6. Use Logarithmic Properties:
Using the property of logarithms that loga(b)−loga(c)=loga(bc):
log10(IRIN)=6.5
7. Convert from Logarithmic to Exponential Form:
Converting from logarithmic form to exponential form gives:
IRIN=106.5
8. Calculate the Ratio:
Evaluating 106.5:
106.5=106×100.5=1,000,000×3.162=3,162,000
Thus, the ratio of signal intensity to noise intensity is:
IRIN≈3.16×106
Final Answer:
The ratio of signal intensity to noise intensity is approximately 3.16×106.
---
The loudness in decibels (dB) is given by the formula:
L=10log10(II0)
where I is the intensity of the signal and I0 is a reference intensity (usually 10−12W/m2).
Let IR be the intensity of the radio signal and IN be the intensity of the noise signal. The loudness of the radio signal (LR) and the noise signal (LN) can be expressed as:
LR=10log10(IRI0)
LN=10log10(INI0)
According to the problem, the difference in loudness is given as:
LR−LN=65dB
Substitute the expressions for LR and LN into the equation:
10log10(IRI0)−10log10(INI0)=65
Dividing the entire equation by 10 gives:
log10(IRI0)−log10(INI0)=6.5
Using the property of logarithms that loga(b)−loga(c)=loga(bc):
log10(IRIN)=6.5
Converting from logarithmic form to exponential form gives:
IRIN=106.5
Evaluating 106.5:
106.5=106×100.5=1,000,000×3.162=3,162,000
Thus, the ratio of signal intensity to noise intensity is:
IRIN≈3.16×106
The ratio of signal intensity to noise intensity is approximately 3.16×106.
Topper's Solved these Questions
- WAVES Book:PHYSICS GALAXY - ASHISH ARORAChapter:WAVES Exercise:Practice Exercise 6.5
Explore 16 Videos
- WAVES Book:PHYSICS GALAXY - ASHISH ARORAChapter:WAVES Exercise:Practice Exercise 6.6
Explore 15 Videos
- WAVES Book:PHYSICS GALAXY - ASHISH ARORAChapter:WAVES Exercise:Practice Exercise 6.3
Explore 11 Videos
- WAVE OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:WAVE OPTICSExercise:Unsolved Numerical Problems
Explore 28 Videos
- X-RAYSBook:PHYSICS GALAXY - ASHISH ARORAChapter:X-RAYSExercise:Unsolved Numerica Problem for Preparation
Explore 23 Videos
Similar Questions
Knowledge Check
Radio waves with frequencies higher than television signals are
Aultrasonic wavesBsound wavesClight wavesDmicrowaves
A radio antenna of 30m. The acceptor is on the ground Rearth=6400km. What is the area covered for signalling
View SolutionWhat travels faster : a radio signal or sound in air ?
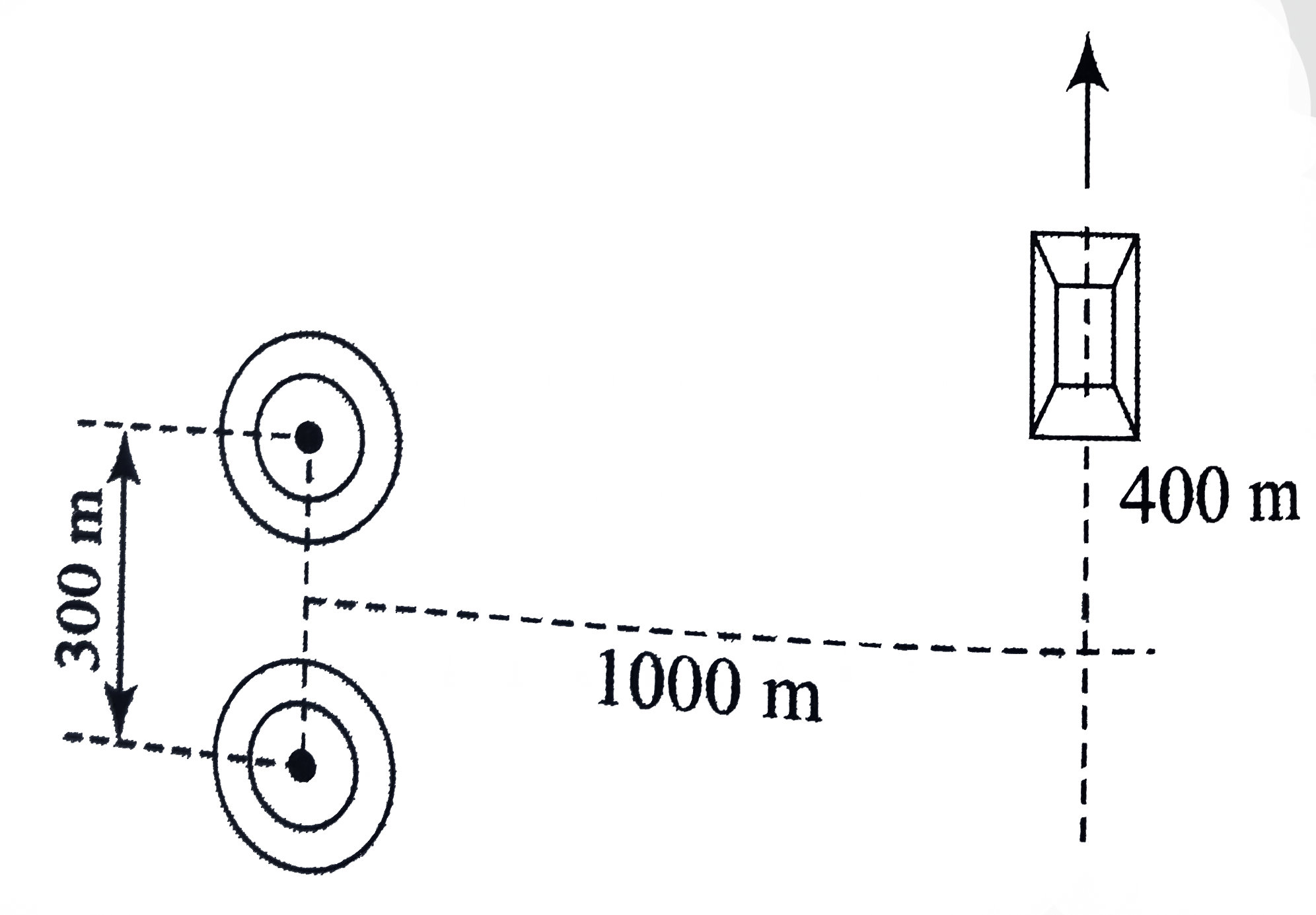
View SolutionTwo radio antennas separated by 300 m as shown in figure simultaneously broadcast indentical singals at the same wavelength. A radio in a car traveling due north receives the signals. (a) If the car is at the position of the second maximum, what is the wavelength of the signals? (b) How much farther must the car travel to encounter the next mininum in reception? (Note: Do not use the small- angle approximation in this problem.)
View SolutionExplain that microwaves are better carriers of signals than radio waves?
View SolutionExplain that microwaves are better carriers of signals than radio waves?
View SolutionDemodulation is the reverse process of modulation, which is performed in a receiver to recover the original modulating signals. At the receiving end, the signals are generally weak due to attenuation in the channel. The receiver selects only the desired signal, rejecting the unwanted (noise) signals and amplifies the same.
Read the above passage and answer the following questions:
(i) What are the main functions of a demodulator?
(ii) Give any two examples of demodulators.
(iii) What does the phenomemom of demodulation imply in day to day life?
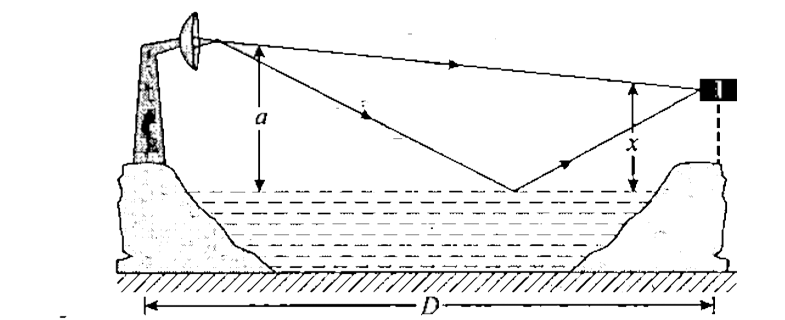
View SolutionIn figure-6.9, a microwave transmitter a height a above the water level of a wide lake transmits microwaves of wavelength λ towards a receiver on the opposite shore, a distance x above the water level. The microwaves reflecting from the water interface with the microwaves arriving directly from the transmitter. Assuming that the lake width D is much greater than a and x, that λ>>a, at what values of x is the signal at the receiver maximum?
View Solution