From the top of a tower h m high, angles of depression of two objects, which are in line with the foot of the tower are α and β(β>α). Find the distance between the two objects.
Let the distance betweeen two objects is x m. and CD=y m.
Given that, ∠BAX=α=∠ABD, [alternate angles]
∠CAY=β=∠ACD (alternate angles)
and the height of the tower, AD=h m
Now, in ΔACD,
tanβ=ADCD=hy
⇒y=htanβ..............(i)
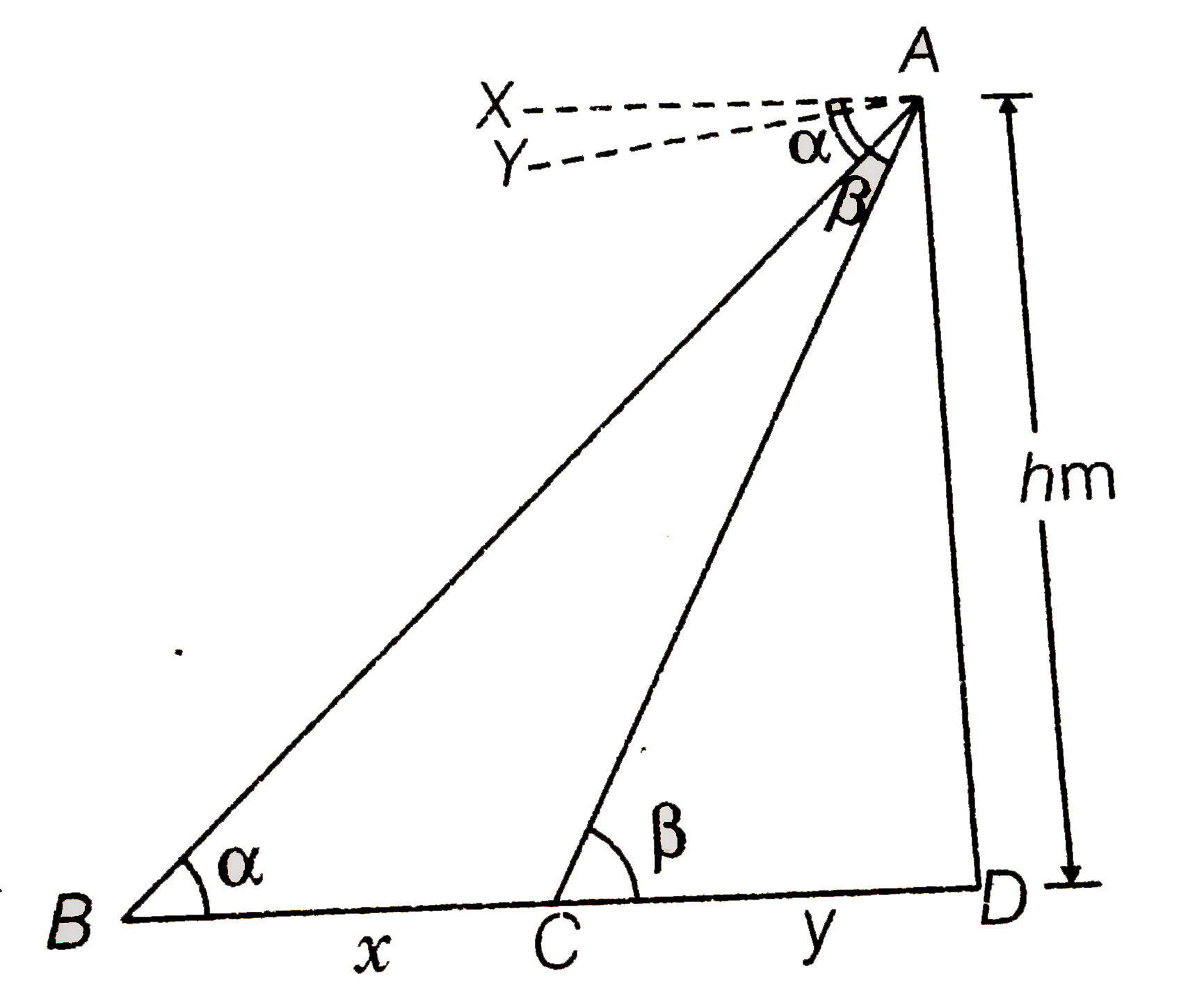
and in ΔABD,
tanα=ADBD⇒=ADBC+CD
⇒tanα=hx+y⇒x+y=htanα
⇒y=htanα−x
From Eqs. (i) and (ii),
htanβ=htanα−x
x=htanα−htanβ
=h(1tanα−1tanβ)=h(cotα−cotβ) [∴cotθ=1tanθ]
Which is required distance between the two objects. Hence Proved.
Topper's Solved these Questions
Similar Questions
From the top of a tower, the angles of depression of two objects on the same side of the tower are found to be α and β(α>β).If the distance between the objects is p metres, show that the height h of the tower is given by h=ptanαtanβtanα−tanβ metres.
View SolutionFrom the top of a 96 m tower, the angles of depression of two cars, on the same side of the tower are α and βrespectively. If tanα=14 and tanβ=17, then find the distance between two cars.
View Solution
Knowledge Check
From the top of a tower of height 180 m the angles of depression of two objects on either sides of the tower are 30∘and45∘ . Then the distance between the objects are
A180(3+√3)mB180(3−√3)mC180(√3−1)mD180(√3+1)mFrom the top of a tower 100 m heigh, the angles of depression of two objects 200 m apart on the horizontal plane and in a line passing through the foot of the tower and on the same side of the tower are 45∘−Aand45∘+A, then angle A is equal to
A15∘B22.5∘C30∘D35∘From a tower 125 metres high the angle of depression of two objects ,which are in horizontal line through the base of the tower , are 45∘and30∘ and they are on the same side of the tower The distance (in metres) between the objects is
A125√3B125(√3−1)C125/(√3−1)D125(√3+1)
There are two points on the horizontal line passing through the foot of a tower in the same side of the tower. The angle of depression of these point from the top of the tower are 45∘ and 60∘ respectively. Find the distance between the two point if the height if the tower is 150 metres.
View SolutionFrom te top of a tower , 60 meters high, the angles of depression of the top and bottom of a pole are αandβ respectively .Find the height of the pole.
View SolutionThe angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top of the second tower from the foot of the first tower is 30∘. Find the distance between the two towers and also the height of the other tower.
View SolutionThe angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top of the second tower from the foot of the first tower is 30∘. Find the distance between the two and also the height of the tower.
View SolutionFrom the top of a tower, the angles of depression of two objects P and Q (situated on the ground on the same side of the tower) separated at a distance of 100(3−√3) m are 45∘and60∘ respectively. The height of the tower is
View Solution
