Two spherical black bodies A and B,having radii $r_{A}$ and $r_{B} = 2 r_{A}$ emit radiation with peak intensities at wavelength 400 nm and 800 nm respectively. If their temperature are $T_{A}$ and $T_{B}$ respectively in Kelvin scale, their emissive powers are $E_{A}$ and $E_{B}$ then :

A

$\frac{T_{A}}{T_{B}} = 2$

B

$\frac{T_{A}}{T_{B}} = 4$

C

$\frac{E_{A}}{E_{B}} = 8$

D

$\frac{E_{A}}{E_{B}} = 4$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:A, D

To solve the problem, we will use Wien's Displacement Law and Stefan-Boltzmann Law. Let's break down the solution step-by-step.
Step 1: Apply Wien's Displacement Law
Wien's Displacement Law states that the product of the peak wavelength of emission ( $λ_{m a x}$ ) and the absolute temperature ( $T$ ) of a black body is a constant. Mathematically, it can be expressed as:
$λ_{m a x} \cdot T = b$
where $b$ is Wien's displacement constant.
For bodies A and B, we have:
$λ_{m a x, A} \cdot T_{A} = λ_{m a x, B} \cdot T_{B}$
Given:
- $λ_{m a x, A} = 400 nm$
- $λ_{m a x, B} = 800 nm$
Substituting these values into the equation gives:
$400 \cdot T_{A} = 800 \cdot T_{B}$
Step 2: Simplify the Equation
We can simplify the equation from Step 1:
$\frac{T_{A}}{T_{B}} = \frac{800}{400} = 2$
This means:
$T_{A} = 2 T_{B}$
Step 3: Use Stefan-Boltzmann Law
The Stefan-Boltzmann Law states that the emissive power $E$ of a black body is proportional to the fourth power of its absolute temperature and its surface area:
$E \propto A \cdot T^{4}$
The surface area $A$ of a sphere is given by:
$A = 4 π r^{2}$
For bodies A and B, the emissive powers can be expressed as:
$E_{A} \propto 4 π r_{A}^{2} \cdot T_{A}^{4}$
$E_{B} \propto 4 π r_{B}^{2} \cdot T_{B}^{4}$
Step 4: Calculate the Ratio of Emissive Powers
To find the ratio of emissive powers $\frac{E_{A}}{E_{B}}$ :
$\frac{E_{A}}{E_{B}} = \frac{4 π r_{A}^{2} \cdot T_{A}^{4}}{4 π r_{B}^{2} \cdot T_{B}^{4}}$
The $4 π$ cancels out:
$\frac{E_{A}}{E_{B}} = \frac{r_{A}^{2} \cdot T_{A}^{4}}{r_{B}^{2} \cdot T_{B}^{4}}$
Given $r_{B} = 2 r_{A}$ :
$\frac{E_{A}}{E_{B}} = \frac{r_{A}^{2} \cdot T_{A}^{4}}{(2 r_{A})^{2} \cdot T_{B}^{4}}$
This simplifies to:
$\frac{E_{A}}{E_{B}} = \frac{r_{A}^{2} \cdot T_{A}^{4}}{4 r_{A}^{2} \cdot T_{B}^{4}} = \frac{T_{A}^{4}}{4 T_{B}^{4}}$
Step 5: Substitute $T_{A}$ in Terms of $T_{B}$
From Step 2, we know $T_{A} = 2 T_{B}$ :
$\frac{E_{A}}{E_{B}} = \frac{(2 T_{B})^{4}}{4 T_{B}^{4}} = \frac{16 T_{B}^{4}}{4 T_{B}^{4}} = 4$
Final Result
Thus, the ratio of the emissive powers of bodies A and B is:
$\frac{E_{A}}{E_{B}} = 4$

|

Updated on:18/9/2024

Class 12 PHYSICS HEAT TRANSFER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two spheres A and B having radii 3 cm and 5 cm respectively are coated with carbon black on their outer surfaces. The wavelengths of maximum intensity of emitted radiation are 300 nm and 500 nm respectively. If the powers radiated are $Q_{A}$ and $Q_{B}$ respectively, then $\frac{Q_{A}}{Q_{B}}$ is
A $\sqrt{\frac{5}{3}}$
B $\frac{5}{3}$
C ${(\frac{5}{3})}^{2}$
D ${(\frac{5}{3})}^{4}$
Question 2 - Select One
The plots of intensity versus wavelength for three black bodies at temperature $T_{1}, T_{2} and T_{3}$ respectively are as shown. Their temperatures are such that

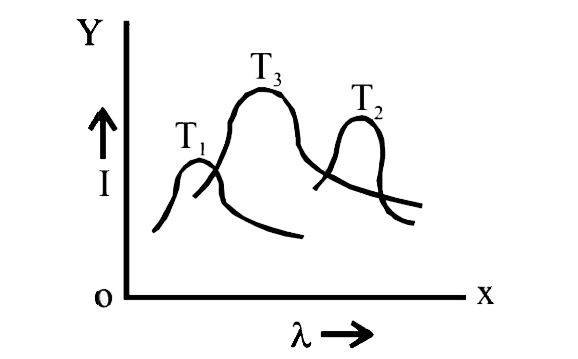A $T_{1} > T_{2} > T_{3}$
B $T_{1} > T_{3} > T_{2}$
C $T_{2} > T_{3} > T_{1}$
D $T_{3} > T_{2} > T_{1}$
Question 3 - Select One
If two gases A and B and temperatures $T_{A}$ and $T_{B}$ respectively have identical Maxwellian plots, then which of the following statements is true?
A $T_{B} = T_{A}$
B $M_{B} = M_{A}$
C $\frac{T_{A}}{M_{B}} = \frac{T_{B}}{M_{A}}$
DGases A and B may be $O_{2}$ and $S O_{2}$ at $27^{\circ} C$ and $327^{\circ} C$ respectively.

PHYSICS GALAXY - ASHISH ARORA-HEAT TRANSFER -Advance MCQs with One or More Option Correct

Home
Ask Doubt
Profile