The graph shows how temperature varies with distance along a well-insulated metal rod which is conducting thermal energy at a steady rate. The slope of this graph is the temperature gradient. There is an analogy between electrical conduction and thermal energy conduction. If an equivalent electrical-graph were to be drawn, which electrical quantity,when plotted against distance along the rod, would have the slope shown. ?
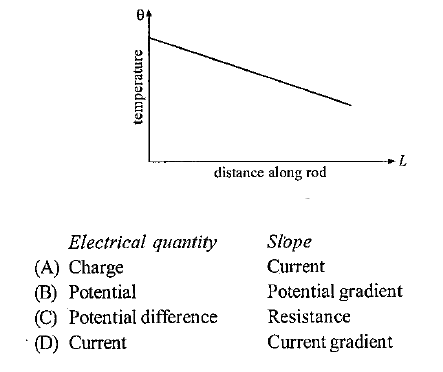
The correct Answer is:B
Electrical quantity anlogous to the temperature is electric potentialand the slope is rate of variation of potential with length which is potential gradient.
Topper's Solved these Questions
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Numerical MCQs Single Options Correct
94 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Advance MCQs with One or More Option Correct
20 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Discussion Question
26 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
64 Videos
Similar Questions
Two spheres of radii R1 and R2 are made of the same material and are at the same temperature. The ratio of their thermal capacities is:
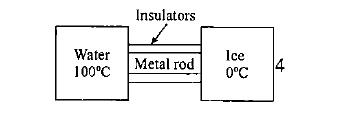
View SolutionAn insulated container is filled with ice at 0∘C, and another container is filled with water that is continuously boiling at 100∘C. In series of experiments, the container connected by various, thick metal rods that pass through the walls of container as shown in the figure-4.46.
In the experiment- I: A copper rod is used and all ice melts is 20 minutes.
In the experiment - II: A steel rod of identical dimensions is used and all melts in 80 minutes.
In the experiment-III: Both the are used in parallel all ice melts in t10 minutes.
In the cxperiment-IV: Both rods are used in parallel all ice melts in t20
View SolutionExplain why the surface of a lake freezes first.
View SolutionIn a vertical U-tube containing a luquid, the two arms are maintained at different temperatures, t1 and t2 . The liquid coplumns in the two arms have heights l1 and l2 respectively. The coefficient of volume expansion of the liquid is equal to

View SolutionAn electron tube was sealed off during manufacture at a pressure of 1.2×10−7 mm of mercury at 27∘C. Its volume is 100 cm3. The number of molecules that remain in the tube is
View SolutionElectrical Analogy For Thermal Conduction
View SolutionAn irregular rod of same uniform material as shown in is conducting heat at a steady rate. The temperature gradient at varoius sections versus area of cross section graph will be
 .
.
View SolutionAn irregular rod of same uniform material as shown in figure is conducting heat at a steady rate. The temperature gradient at various sections versus area of cross section graph will be
_S01_094_Q01.png)
View SolutionTwo different rods A and B are kept as shown in figure . The variation of temperature of different cross sections with distance is plotted in a graph shown in figure . The ration of thermal conductivities of A and B is -
View Solutionकिसी छड़ में ऊष्मा चालन के सन्दर्भ में निम्न को स्पष्ट कीजिये -
(i) समतापी पृष्ठ, (ii) ताप प्रवणता, (iii) उष्मीय चालकता गुणांक |
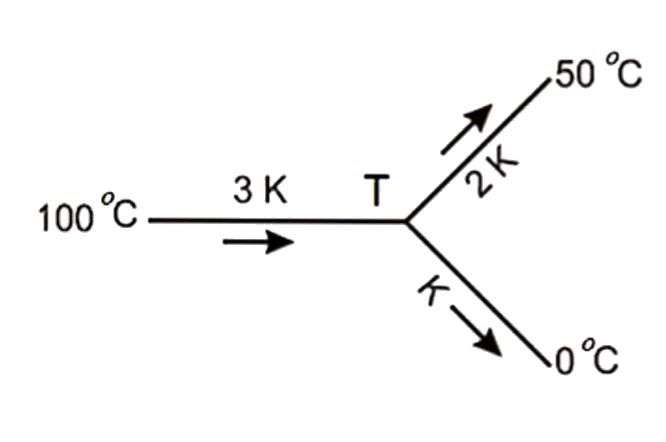
View SolutionThree rods of the same dimension have thermal conductivity 3K, 2K and K as shown in the figure. The temperature of the junction in steady-state is
View SolutionA graph is drawn between centigrade temperatures of a body along x-axis and corresponding Fahrenheit temperatures along y-axis. Slope of the graph is
View SolutionHow does electrical conductivity vary in metals with temperature?
View SolutionExplain the following in reference to thermal conduction in a rod: Temperature gradient.
View SolutionIf K and sigma respectively are the thermal and electrical conductivities of a metal absolute temperature T, then:
View Solution
