Acubical container of side a and wall thickness x (a: « a) is suspendedin air and filled n molesof diatomic gas (adiabatic exponent=y) inaroom where room temperature isT^. Ifat/ = 0 gastemperature is Fj (F, > Fq), find the gas temperature as a function of time t. Assume the heat is conducted through all the walls ofcontainer.
To solve the problem, we need to find the gas temperature T as a function of time t for a cubical container filled with diatomic gas. The process involves understanding heat conduction through the walls of the container and how it affects the temperature of the gas inside.
1. Understanding the Setup:
- We have a cubical container with side length a and wall thickness x.
- The container is filled with n moles of a diatomic gas, which has an adiabatic exponent γ=75.
- The initial temperature of the gas at t=0 is T1, and the room temperature is T0 (where T1>T0).
2. Heat Loss Due to Conduction:
- The rate of heat loss due to conduction through the walls of the container can be expressed as:
dqdt=k⋅A⋅(T−T0)x
- Here, A is the surface area of the container, which for a cube is 6a2.
3. Expression for Heat Transfer:
- Substituting the area into the equation gives:
dqdt=k⋅6a2⋅(T−T0)x
4. Change in Internal Energy:
- The heat lost dq also relates to the change in temperature of the gas:
dq=nR(γ−1)dT
- Here, R is the universal gas constant.
5. Equating Heat Loss and Change in Internal Energy:
- Setting the two expressions for dq equal gives:
nR(γ−1)dT=−k⋅6a2⋅(T−T0)xdt
6. Rearranging the Equation:
- Rearranging the equation yields:
dT(T−T0)=−6ka2(γ−1)nRxdt
7. Integrating Both Sides:
- Integrate both sides:
∫dT(T−T0)=−6ka2(γ−1)nRx∫dt
- The left side integrates to ln|T−T0|, and the right side integrates to −6ka2(γ−1)nRxt+C.
8. Applying Initial Conditions:
- At t=0, T=T1:
ln|T1−T0|=C
- Therefore, we can express C in terms of T1.
9. Final Expression:
- Substitute C back into the integrated equation:
ln|T−T0|=−6ka2(γ−1)nRxt+ln|T1−T0|
- Exponentiating both sides gives:
|T−T0|=|T1−T0|e−6ka2(γ−1)nRxt
- Thus, the gas temperature as a function of time t is:
T(t)=T0+(T1−T0)e−6ka2(γ−1)nRxt
- We have a cubical container with side length a and wall thickness x.
- The container is filled with n moles of a diatomic gas, which has an adiabatic exponent γ=75.
- The initial temperature of the gas at t=0 is T1, and the room temperature is T0 (where T1>T0).
- The rate of heat loss due to conduction through the walls of the container can be expressed as:
dqdt=k⋅A⋅(T−T0)x
- Here, A is the surface area of the container, which for a cube is 6a2.
- Substituting the area into the equation gives:
dqdt=k⋅6a2⋅(T−T0)x
- The heat lost dq also relates to the change in temperature of the gas:
dq=nR(γ−1)dT
- Here, R is the universal gas constant.
- Setting the two expressions for dq equal gives:
nR(γ−1)dT=−k⋅6a2⋅(T−T0)xdt
- Rearranging the equation yields:
dT(T−T0)=−6ka2(γ−1)nRxdt
- Integrate both sides:
∫dT(T−T0)=−6ka2(γ−1)nRx∫dt
- The left side integrates to ln|T−T0|, and the right side integrates to −6ka2(γ−1)nRxt+C.
- At t=0, T=T1:
ln|T1−T0|=C
- Therefore, we can express C in terms of T1.
- Substitute C back into the integrated equation:
ln|T−T0|=−6ka2(γ−1)nRxt+ln|T1−T0|
- Exponentiating both sides gives:
|T−T0|=|T1−T0|e−6ka2(γ−1)nRxt
- Thus, the gas temperature as a function of time t is:
T(t)=T0+(T1−T0)e−6ka2(γ−1)nRxt
Topper's Solved these Questions
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.11
1 Video
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.12
1 Video
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.9
1 Video
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
64 Videos
Similar Questions
A heat-conducting piston can freely move inside a closed thermally insulated cylinder with an ideal gas. In equilibrium the piston divides the cylinder into two equal parts, the gas temperature being equal to T0. The piston is slowly displaced. Find the gas temperature as a function of the ratio η of the volumes of the greater and smaller sections. The adiabatic exponent of the gas is equal to γ.
View SolutionAn adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T0 and pressure P0 occupies a volume V0 in the cylinder. The atmospheric pressure is P0 and the atmospheric temperature is T1(>T0). Find
(a) the temperature of the gas as a function of time
(b) the height raised by the piston as a function of time.
Neglect friction and heat capacities of the container and the piston.
View Solution
Knowledge Check
Figure shows a long cylindrical container with ideal gas in two chambers. Lower chamber is filled with one mole of a mono atomic gas, while upper chamber has one mole of a diatomic gas. The gases initially are at temperature 300K, the container walls as well as pistons are conducting. Both the pistons are identical with mass 'M' and area 'A' such that MgA=P0 (atmosphere pressure).
Assuming the ideal gas constant to be R, answer the following questions:

Total work done by the ideal gases in this process isA300Rln(3)B300Rln(95)CzeroD300Rln(2)
(i) A conducting piston divides a closed thermally insulated cylinder into two equal parts. The piston can slide inside the cylinder without friction. The two parts of the cylinder contain equal number of moles of an ideal gas at temperature T0. An external agent slowly moves the piston so as to increase the volume of one part and decrease that of the other. Write the gas temperature as a function of ratio (β) of the volumes of the larger and the smaller parts. The adiabatic exponent of the gas is γ.
(ii) In a closed container of volume V there is a mixture of oxygen and helium gases. The total mass of gas in the container is m gram. When Q amount of heat is added to the gas mixture its temperature rises by ΔT. Calculate change in pressure of the gas.
View SolutionA spherical container made of non conducting wall has a small orifice in it. Initially air is filled in it at atmospheric pressure (P0) and atmospheric temperature (T0). Using a small heater, heat is slowly supplied to the air inside the container at a constant rate of H J/s. Assuming air to be an ideal diatomic gas find its temperature as a function of time inside the container.
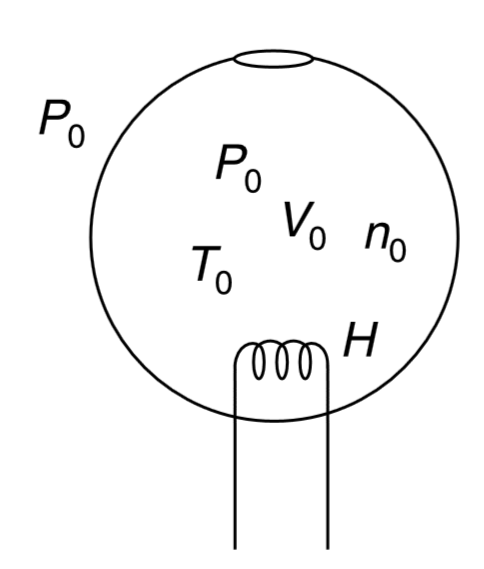
View Solutionmonatomic ideal gas is contained in a rigid container of volume V with walls of totsl inner surface area A, thickness x and thermal condctivity K. The gas is at an initial temperature t0 and pressure P0 . Find tjr pressure of the gas as a function of time if the temperature of the surrounding air is Ts . All temperature are in absolute scale.
View SolutionAn ideal gas of molar mass M is enclosed in a vessel of volume of V whose thin walls are kept at a constant temperature T. At a moment t=0 a small hole of area S is opened, and the gas starts escaping into vacuum. Find the gas concentration n as a function of time t if at the initial moment n(0)=n0.
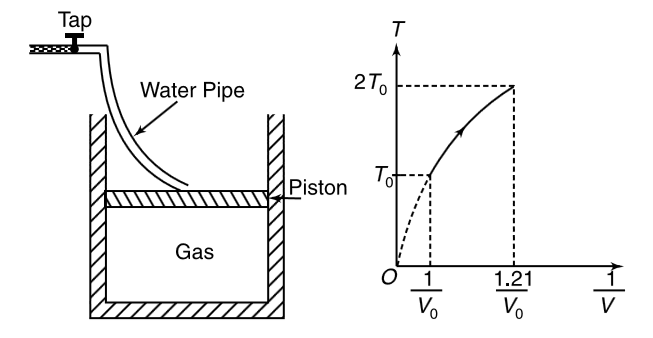
View SolutionA cylindrical container has insulating wall and an insulating piston which can freely move up and down without any friction. It contains a mixture of ideal gases. Originally the gas is at atmospheric pressure P0 and temperature (T0). A tap positioned above the container is opened and it supplies water at a constant rate of dmdt=0.25kg/s. The water collects above the piston in the container and the gas compresses. The tap is kept open till the temperature of the gas is doubled. During the process the T vs 1V graph for the gas was recorded and found to be a parabola with its vertex at origin as shown in the graph. Area of piston A=1.515×10−3m2 and atmospheric pressure =105N/m2
(a) Find the ratio of Vrms and speed of sound in the gaseous mixture.
(b) For how much time the tap was kept open?
View SolutionFigure shows water in a container having 2.0−mm thick walls made of a material of thermal conductivity 0.50Wm−1^(@)C^(-1).Theconta∈eriskept∈ame<∈g−icebathat0^(@)C.The→talsurfacearea∈contactwithwateris0.05m^(2).Awheelisclamped∈sthewaterandiscoup≤→ablockofmassMasshowm∈thefigure.Asthegoesdown,thewheelrotates.Itisfoundtˆafterso±etimeasteadystateisreached∈whichtheblockgoesdonwwithacontantspeedof10cm^(-1)andthetemperatureofthewaaterrema∈scontantat1.0^(@)C.F∈dthemassMoftheblock.As∑etˆtheheatflowoutofthewateronlythroughthewalls∈contact.Takeg=10ms^(-2) .

View SolutionA cubical container having each sides as l is filled with a gas having N molecules in the container. Mass of each molecule is m. If we assume that at every instant half of the molecules are moving towards the positive x-axis and half of the molecules are moving towards the negative x-axis.Two walls of the container are perpendicular to the x-axis. Find the net force acting on the two walls given? Assume that all the molecules are moving with speed v0.
View Solution