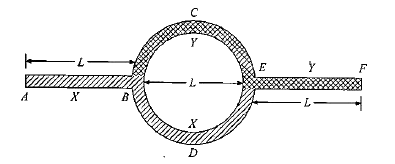
Three rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C. Calculate the temperature of the junction B, C and D. The thermal conductivity of X is 0.92cal/sec−cm∘C and that of Y is 0.46cal/sec−cm−∘C.
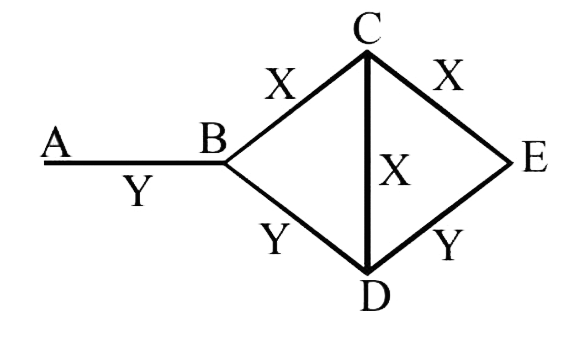
Let kx and ky be the thermal conductivities of X and Y respectively and let TB,TC and TD be the temperatures of junctionsB,CandDrespectively. Given TA=60∘C andTE=10∘C.
In order to solvethis problem, wewill applythe principle that, in the steady state, the rate at which heat enters a junction is equal to the rate at which heat leavesthat junction. In Figure- 4.18 the direction offlow ofheat is given by arrows.
For junction B, we have
kyA(TA−TB)d=kxA(TB−TC)d+kyA(TB−TD)d
or ky(TA−TB)=kx(TB−TC)+ky(TB−TD)
or (TA−TB)=kxky(TB−TC)+ky(TB−TD)
Given kxky=9.2×10−24.6×10−2=2
and TA=60∘C.
Therefore, (60−TB)=2(TB−TC)+(TB−TD)
or 4TB−2TC−TD=60
For junction C, we have
kxA(TB−TC)d=kxA(TC−TD)d+kxA(TC−TE)d
Solving we get
−TB+3TC−TD=10 [AtTE=10∘] ....(4.26)
For junction D, we have
or kyA(TB−TD)d+kxA(TC−TD)d=kYA(TD−TE)d
or (TB−TD)+kxky(TC−TD)+(TD−TE)
Putting kxky=2 and TE=10∘C in this equation , we have
(TB−TD)+2(TC−TD)=(TD−10)
TB+2TC−4TD=−10 ...(4.27)
Solving equation (4.25),(4.26) and (4.27), we get
TB=30∘C
and TC=TD=20∘C .
Topper's Solved these Questions
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.13
1 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.14
1 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.11
1 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
64 Videos
Similar Questions
Three rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C. Calculate the temperature of the junction B, C and D. The thermal conductivity of X is 0.92cal/sec−cm∘C and that of Y is 0.46cal/sec−cm−∘C.

View SolutionThree rods of material x and three of material y are connected as shown in figure. All the rods are identical in length and cross sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C , calculate the temperature of the junction B. The thermal conductivity of x is 800Wm−1^(@)C^(-1)andtˆofyis400Wm^(-1)^(∘)C−1 .

View Solution
Knowledge Check
Three rods of material 'x' and three rods of materialy are connected as shown in All the rods are of identical length and cross section If the end A is maintained at 60∘C and the junction E at 10∘0C find effective Thermal Resistance Given length of each rod =1 area of cross-section =A conductivity of x=K and conductivity of y=2K
 .A4l3KAB7l6KAC4KA3lD7KA3l
.A4l3KAB7l6KAC4KA3lD7KA3lSeven identical rods of material of thermal conductivity K are connected as shown in figure. All the rods are of identical length L and cross sectional area A1. If one end A is kept at 100∘C and the other end B is kept at 0∘C, what would be the temperature of the junctions C, D and E (TC,TD and TE) in the steady state?
 ATC>TE>TDBTC=TD=37.5∘C,TE=50∘CCTC=62.5∘C,TD=37.5∘C,TE=50∘CDTC=60∘C,TD=40∘C,TE=50∘C
ATC>TE>TDBTC=TD=37.5∘C,TE=50∘CCTC=62.5∘C,TD=37.5∘C,TE=50∘CDTC=60∘C,TD=40∘C,TE=50∘C
Seven identical rods of material of thermal conductivity k are connected as shown in Fig. All the rods are of identical length l and cross sectional area A If the one end B is kept at 100∘C and the other end is kept at 0∘C what would be the temperatures of the junctions C, D and E(θC,θ)D and θE) in the steady state?AθC>θE>θDBθE=50∘C and θD=37.5∘CCθE=50∘C,θC=62.5∘C and θD=37.5∘CDθE=50∘C,θC=60∘C and θD=40∘C
Two rods of material, x and two of y are connected as shown in the figure. All the rods are indentical in length and cross-sectional area. If the end A is maintained at 80∘C and the end D is maintained at 10∘C, calculate the temperature of the junctions B and C in the steady state. Thermal conductivity of x is double that of y.

View SolutionFew rods of material X and Y are connected as shown in figure - 4.10. The cross sectional area of all the rods are same. If the end A is maintained at 80∘C and the end F is maintained at 10^(@)C~ . Calculate the temperatures of junctions B and E in steady state . Given that thermal conductivty of material X is double that of Y.
View SolutionFour rods of material X and three rods of material Y are connected as shown in figure. All the rods are of identical lengths and cross-sectional area. Given thermal resistance of rod of material X,Rx=R and thermal conductivities of materials are related by relation KY=2KX.
_E01_157_Q01.png)
Column-IColumn-II(A)Thermal resistance between B and E(p)50013.∘C(B)Thermal resistance between A and F(q)70013.∘C(C)Temperature of junction B(r)2R3(D)Temperature of junction D(s)13R6
View SolutionSeven identical rods of matrical of thermal conductivity k are connected as shown in All the rod are of identical length l and cross sectional area A if the one end b is kept at 100∘C and the other end is kept at 0∘C The temperatures of the junctions C,D and E(θDandθE) be in the steady state
 .
.
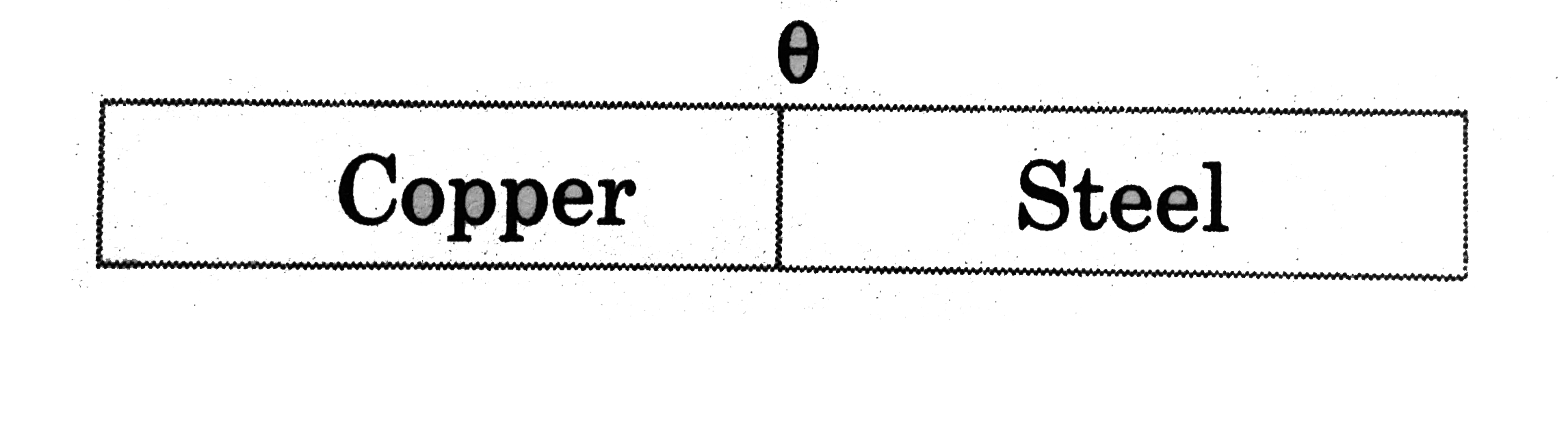
View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and equal cross-sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C. Find the temperature θ at the junction of the rods. Conductivity of copper
=390W/m−∘C and that of steel =46W/m−∘C.
 .
.
View Solution
