A small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
Current I(t), lags voltage V(t) by 90∘
Over a full cycle the capacitor C does not consume any energy from the voltage source.
Current I(t) is in phase with voltage V(t).
Current I(t) leads voltage V(t) by 180∘
The correct Answer is:B
Step by step video & text solution for A small signal voltage V(t)=V_(0)sin omegat is applied across an ideal capacitor C: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Explain the term 'capacitive reactance'.Show graphically the variation of capacitive reactance with frequency of the applied alternating voltage.
An a.c. voltage E=E0sinωt is applied a across a pure capacitor C.Show mathematically that the current flowing through it leads the applied voltage by a phase angle of π/2View SolutionAn alternating voltage V=V0sinωt is applied across a circuit. As a result, a current I=I0sin(ωt–p2) flows in it. The power consumed per cycle is
View Solution
Knowledge Check
- Question 1 - Select One
If an alternating voltage V=V_0 sin omegat is applied across an inductance I, the current through the inductance will be
AI=I0sinωtBI=I0sin(ωt+π/2)CI=I0sin(ωt+π/2)DI=I0sin(ωt+π) - Question 2 - Select One
If an alternating voltage V=V_0 sin omegat is applied across an inductance I, the current through the inductance will be
AI=I0sinωtBI=I0sin(ωt+π/2)CI=I0sin(ωt+π/2)DI=I0sin(ωt+π) - Question 3 - Select One
A sinusoidal voltage V(t) = 100 sin (500t) is applied across a pure inductance of L = 0.02 H. the current through the coil is
A10 cos (500t).B−10 cos (500t).C10 sin (500t)D−10 sin (500t)
An alternating voltage V=V0sinωt is connected to a capacitor of capacity C0 through an AC ammeter of zero resistance. The reading of ammeter is
View SolutionA sinusoidal voltage V(t)=100sin(500t) is applied across a pure inductance of L=0.02H. The current through the coil is :
View SolutionThe alternating emf of e=e0 sin ωt is applied across capacitor C. the current through the circuit is given by
View SolutionWhen a voltage V=V0 cos ωt is applied across a resistor of resistance R, the average power dissipated per cycle in the resistor is given by
View SolutionA time varying voltage V= 2t (Volt) is applied across and ideal inductor of inductance L =2H as shown in Fig. Then (assume current to be zero at t =0)
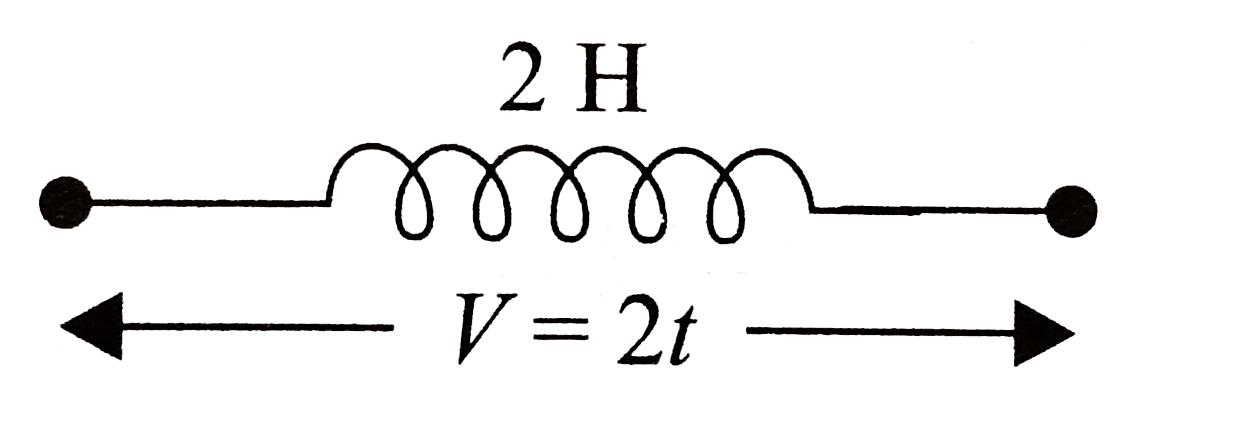 View Solution
View Solution

