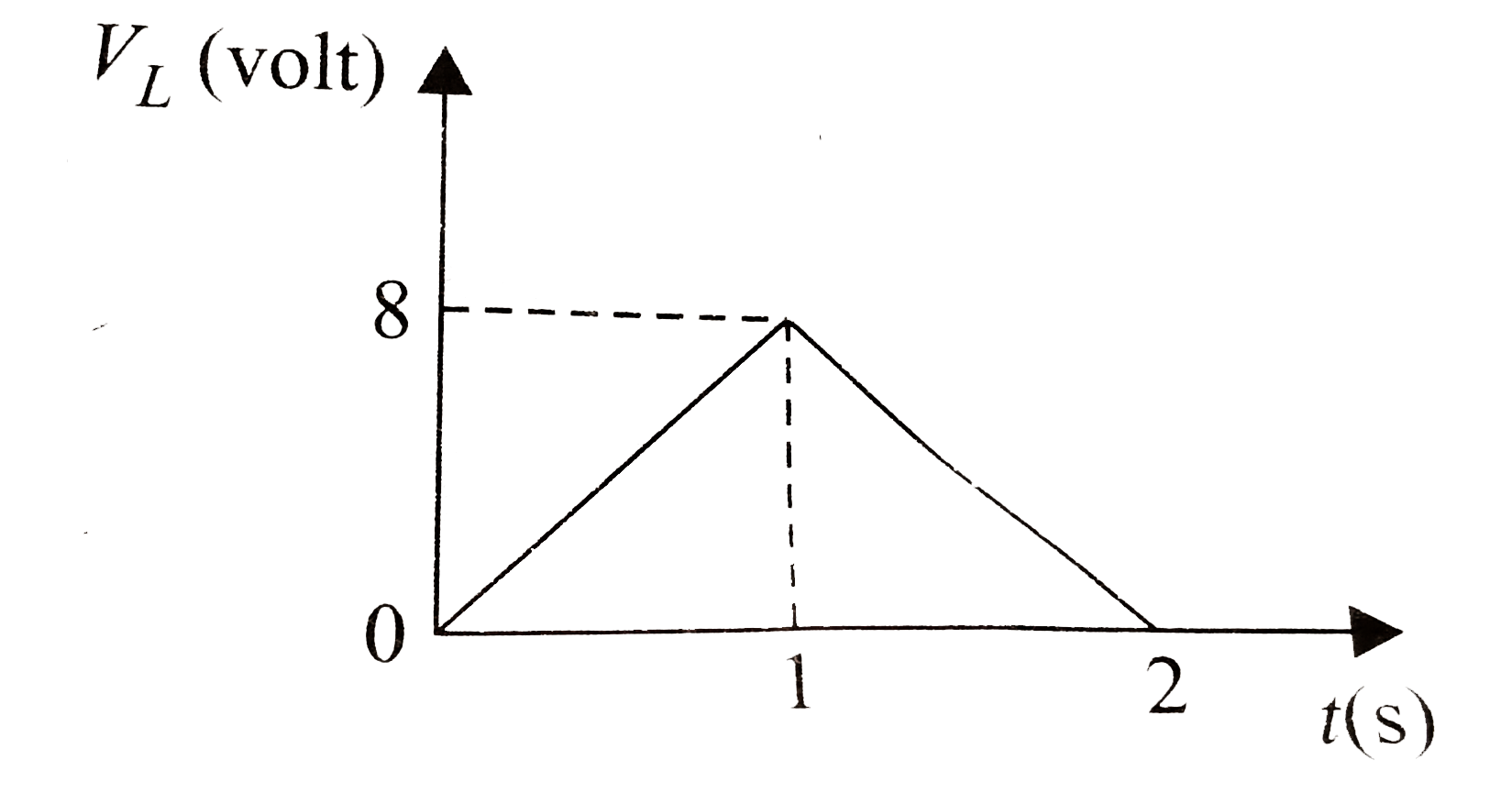
A time varying voltage V= 2t (Volt) is applied across and ideal inductor of inductance L =2H as shown in Fig. Then (assume current to be zero at t =0)

Current versus time graph is a parabola

energy stored in magnetic field at $t = 2 s i s 4 J$ .

Potential energy at time $t = 1 s$ in magnetic field is increasing at a rate of $1 J / s$

energy stored in magnetic field is zero all the time.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C

Updated on:21/07/2023

A small signal voltage $V (t) = V_{0} sin ω t$ is applied across an ideal capacitor $C$ :
ACurrent l(t) leads voltage V(t) by $180^{\circ}$
BCurrent l(t) lags voltage V(t) by $90^{\circ}$
COver a full cycle the capacitor C does not consume any energy from the voltage source
DCurrent l(t) is in phase with voltage V(t)
A small signal voltage $V (t) = V_{0} sin ω t$ is applied across an ideal capacitor $C$ :
ACurrent $I (t)$ , lags voltage $V (t)$ by $90^{\circ}$
BOver a full cycle the capacitor $C$ does not consume any energy from the voltage source.
CCurrent $I (t)$ is in phase with voltage $V (t)$
DCurrent $I (t)$ leads voltage $V (t)$ by $180^{\circ}$
A sinusoidal voltage V(t) = 100 sin $(500 t)$ is applied across a pure inductance of L = 0.02 H. the current through the coil is
A10 cos (500t).
B $- 10$ cos (500t).
C10 sin (500t)
D $- 10$ sin (500t)