A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate $β$ to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :

$\frac{α β}{t (α + β)}$

$\frac{α + β}{α β} t$

$\frac{α β}{α + β} t$

$α β \frac{)}{(α + β)}$

Video Solution

Text Solution

Verified by Experts

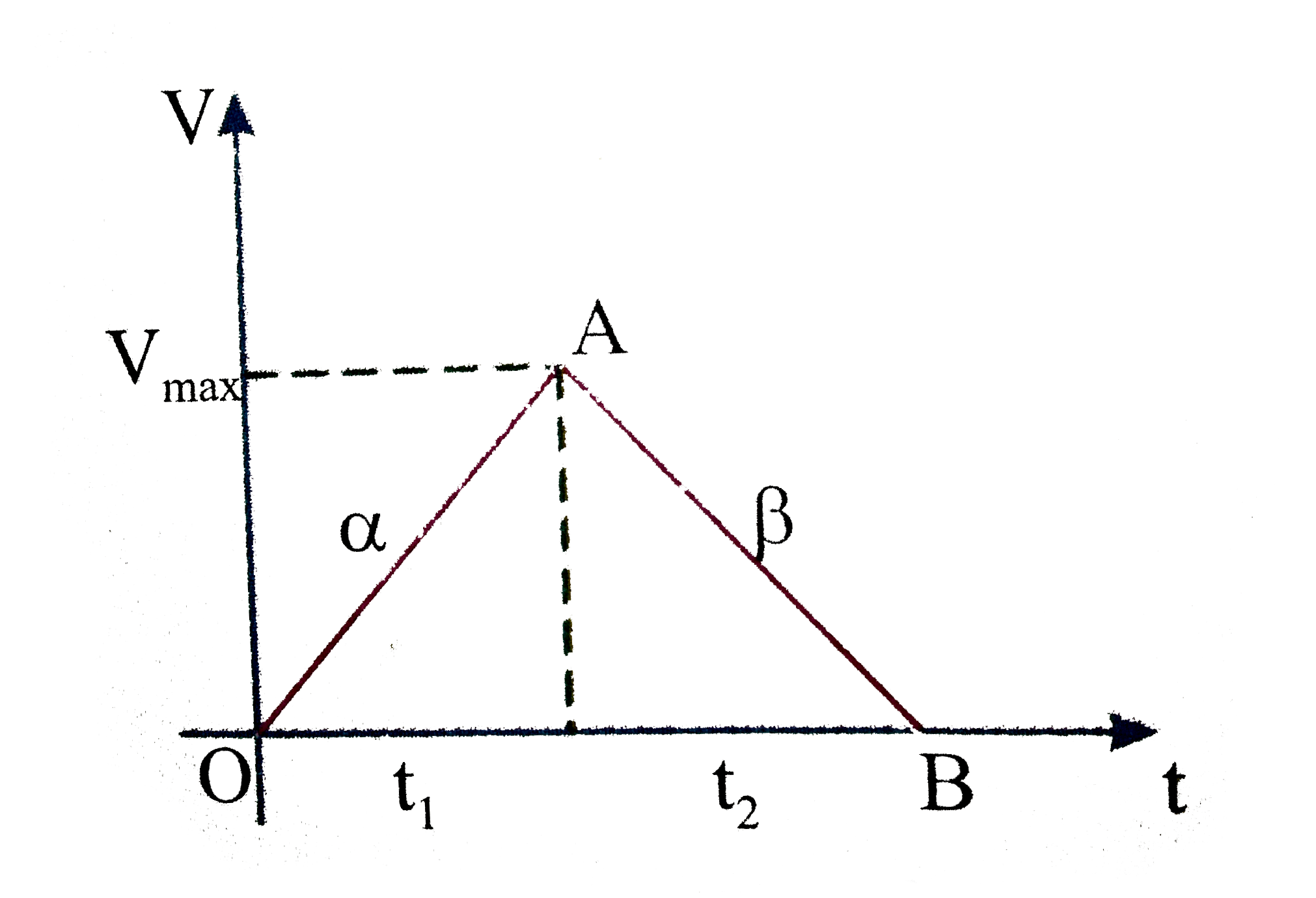
If the car accelerates for time $t_{1}$ and decelerates for time $t_{2}$ , then according to given problems
$t = t_{1} + t_{2}$
If $v_{max}$ is the maximum valocity of the car , then from v/t curve , we have
$α = \frac{V_{max}}{t_{1}}, β = \frac{v_{max}}{t_{2}}$
[as slope of v/t curve gives acceleration.]
so $(\frac{1}{α} + \frac{1}{β}) = \frac{t_{1} + t_{2}}{v_{max}} \Rightarrow V_{max} = \frac{α β}{(α + β)} t$

$[∵ t = t_{1} + t_{2}]$
Hence correct answer is (C) .

Updated on:21/07/2023

A car accelerates from rest at a constant rate $α$ for sometime , after which it decelerates at a constant rate $β$ and comes to rest. If T is the total time elapsed, the maximum velocity acquired by the car is
A $(\frac{α β}{α + β}) T$
B $((α + \frac{β}{α β}) T$
C $(\frac{α^{2} + β^{2}}{α β}) T$
D $\frac{1}{2} \frac{α T}{β}$
A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate $β$ to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
A $\frac{a b}{(a + b)} t$
B $\frac{a b}{(a - b)} t$
C $\frac{a t^{2}}{(a + b)}$
D $\frac{t b^{2}}{(a + b)}$
A car accelerates from rest at a constant rate of $2 m s^{- 2}$ for some time. The it retatds at a constant rate of $4 m s^{- 2}$ and comes to rest. It remains in motion for $6 s$ .
AIts maximum speed is $8 m s^{- 1}$
BIts maximum speed is $6 m s^{- 1}$
CIt travelled a total distance of $24 m$
DIt travelled a total distance of $18 m$