The time constant of a circuit is 10 sec , when a resistance of 10Ω is connected in series in a prevouse circuit then time constant becomes 2 second, then the self inductance of the circuit is :-
2.5 H
5H
15H
25H
The correct Answer is:c
To find the self-inductance of the circuit, we can follow these steps:
Step 1: Understand the Time Constant
The time constant (τ) for an inductive circuit is given by the formula:
τ=LR
where L is the self-inductance and R is the resistance.
Step 2: Set Up the Initial Condition
Initially, the time constant is given as 10 seconds. Let the resistance in the circuit be R. Therefore, we can write:
τ=LR=10(1)
From this, we can express L in terms of R:
L=10R(2)
Step 3: Set Up the Condition with Additional Resistance
When a resistance of 10Ω is added in series, the new equivalent resistance becomes R+10. The new time constant is given as 2 seconds:
τ′=LR+10=2(3)
Step 4: Express L from the New Condition
From equation (3), we can express L as:
L=2(R+10)(4)
Step 5: Equate the Two Expressions for L
Now we have two expressions for L from equations (2) and (4):
1. L=10R
2. L=2(R+10)
Setting these equal to each other:
10R=2(R+10)
Step 6: Solve for R
Expanding the right side:
10R=2R+20
Subtracting 2R from both sides:
8R=20
Dividing both sides by 8:
R=208=2.5Ω
Step 7: Substitute R Back to Find L
Now substituting R back into equation (2) to find L:
L=10R=10×2.5=25H
Final Answer
The self-inductance of the circuit is:
25H
---
The time constant (τ) for an inductive circuit is given by the formula:
τ=LR
where L is the self-inductance and R is the resistance.
Initially, the time constant is given as 10 seconds. Let the resistance in the circuit be R. Therefore, we can write:
τ=LR=10(1)
From this, we can express L in terms of R:
L=10R(2)
When a resistance of 10Ω is added in series, the new equivalent resistance becomes R+10. The new time constant is given as 2 seconds:
τ′=LR+10=2(3)
From equation (3), we can express L as:
L=2(R+10)(4)
Now we have two expressions for L from equations (2) and (4):
1. L=10R
2. L=2(R+10)
10R=2(R+10)
Expanding the right side:
10R=2R+20
Subtracting 2R from both sides:
8R=20
Dividing both sides by 8:
R=208=2.5Ω
Now substituting R back into equation (2) to find L:
L=10R=10×2.5=25H
The self-inductance of the circuit is:
25H
Topper's Solved these Questions
- ELECTRO MAGNETIC INDUCTIONBOOK - MOTIONCHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - EXERCISE-4| Section B (Prevous Years Problems )
29 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - MOTIONCHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - EXERCISE-3 (Assertion & Reasoning)
18 Videos
- Electrical Instrument BOOK - MOTIONCHAPTER - Electrical Instrument EXERCISE - EXERCISE -3
16 Videos
- ELECTRO MAGNETIC WAVES BOOK - MOTIONCHAPTER - ELECTRO MAGNETIC WAVES EXERCISE - EXERCISE - 3 (SECTION - B)
8 Videos
Similar Questions
Knowledge Check
The time constant of C-R circuit is
A1CRBCRCCRDRCThe time constant of the circuit shown is
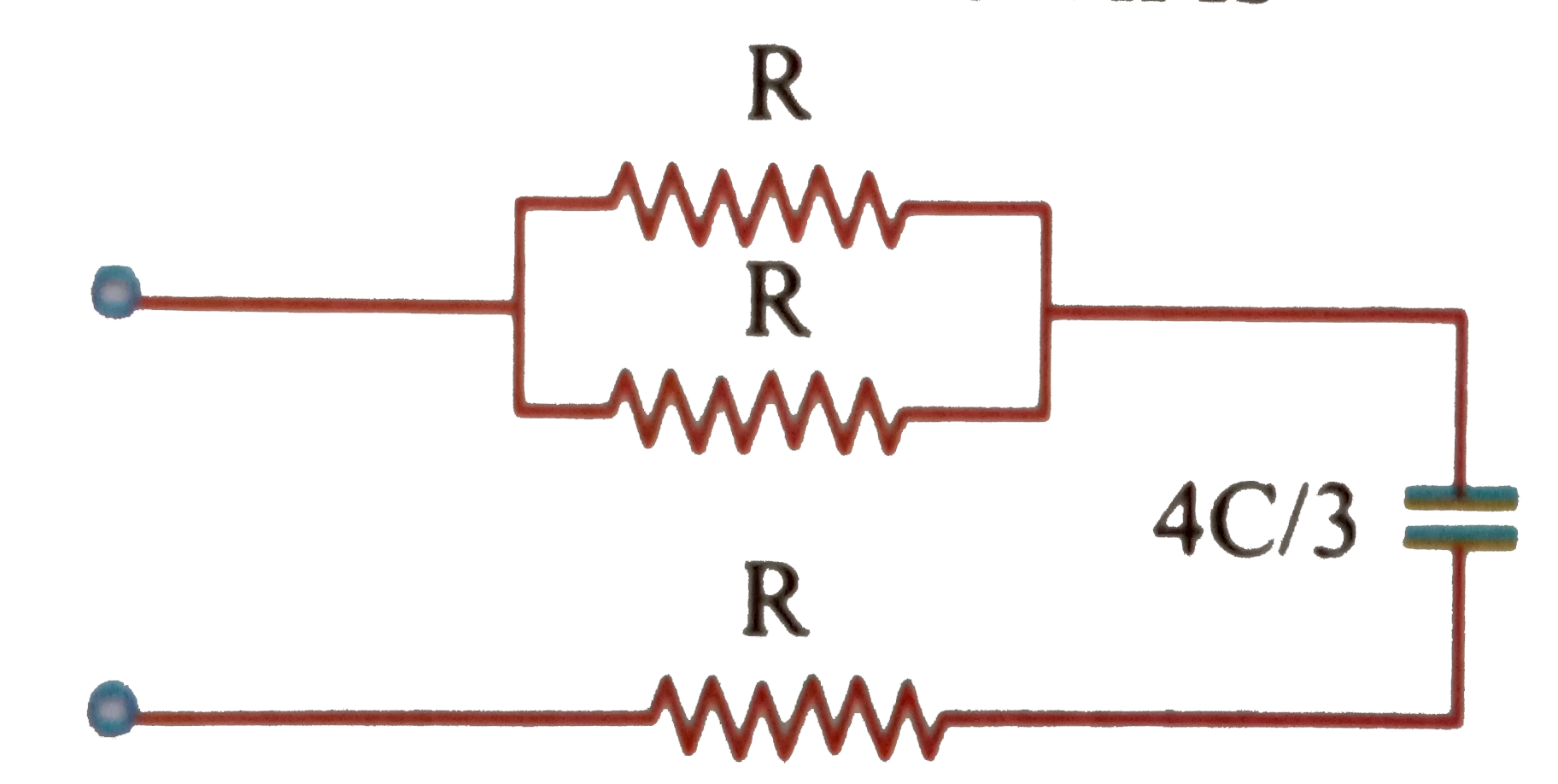 ARCB2RCC3RCD4RC
ARCB2RCC3RCD4RCTime constant of LR circuit will be
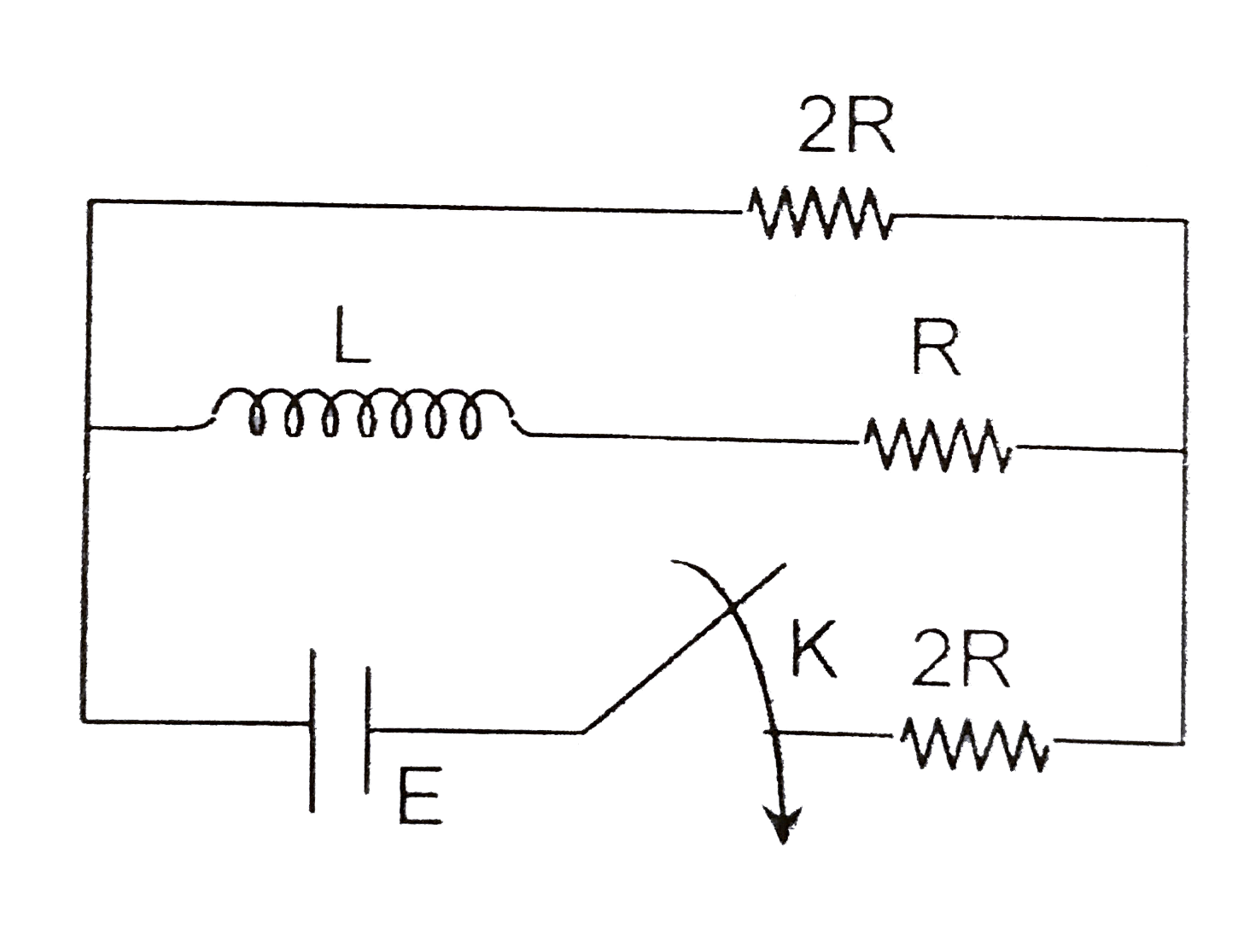 ALRB2LRCL2RDNone of these
ALRB2LRCL2RDNone of these
The time constant for the given circuit is
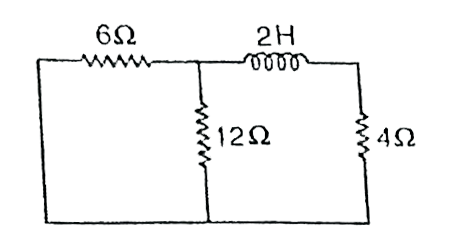
View SolutionThe time constant of the circuit shown in the figure is
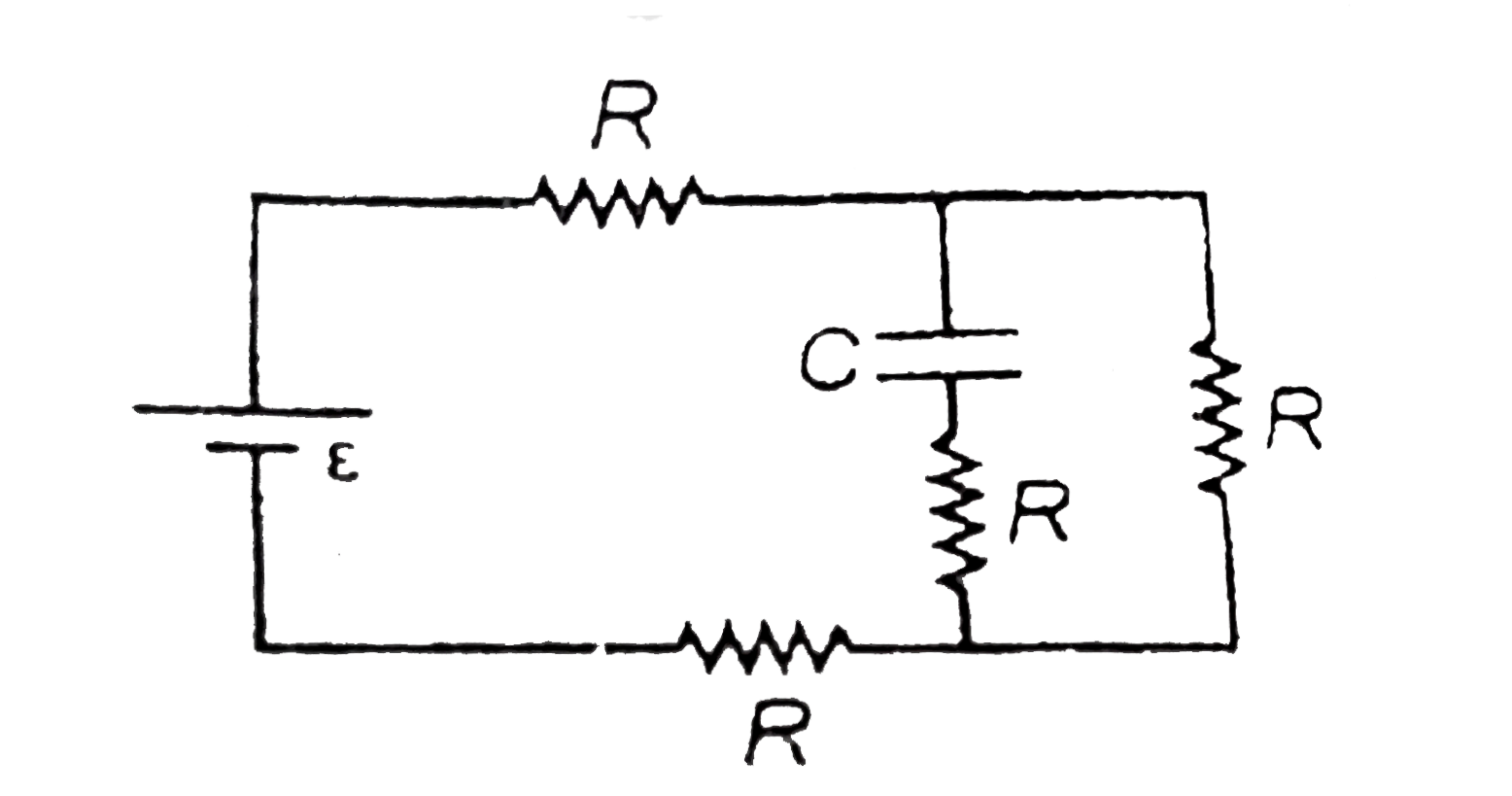
View SolutionThe time constant of the circuit shown in the figure is
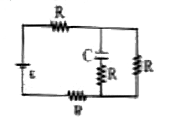
View SolutionFind time constant of given circuit:-
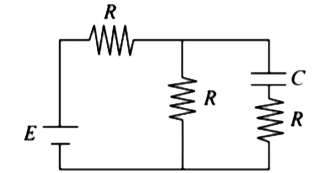
View SolutionIn the transient shown the time constant of the circuit is :
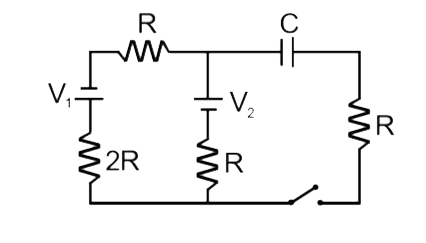
View Solution

