A solenoid of radius R and length L has a current I=I0 cosωt. The value of induced electric field at a distance of r outside the solenoid, is
μ0nI0ωR22rsinωt
μ0nI0ωR2rsinωt
μ0nI0R22rsinωt
Zero
The correct Answer is:a
Step by step video, text & image solution for A solenoid of radius R and length L has a current I = I_0 cosωt. The value of induced electric field at a distance of r outside the solenoid, is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTRO MAGNETIC INDUCTIONBOOK - MOTIONCHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - EXERCISE-4| Section B (Prevous Years Problems )
29 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - MOTIONCHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - EXERCISE-3 (Assertion & Reasoning)
18 Videos
- Electrical Instrument BOOK - MOTIONCHAPTER - Electrical Instrument EXERCISE - EXERCISE -3
16 Videos
- ELECTRO MAGNETIC WAVES BOOK - MOTIONCHAPTER - ELECTRO MAGNETIC WAVES EXERCISE - EXERCISE - 3 (SECTION - B)
8 Videos
Similar Questions
A cylindrical conductor of radius 'R' carries a current 'i'. The value of magnetic field at a point which is R/4 distance inside from the surface is 10T. Find the value of magnetic field at point which is 4R distance outside from the surface
View SolutionA tightly- wound solenoid of radius a and length l has n turns per unit length. It carries an electric current i. Consider a length dx of the solenoid at a distance x from one end. This contains n dx turns and may be approximated as a circular current I n dx. (a) Write the magnetic field at the centre of the solenoid due to this circular current. Integrate this expression under proper limits to find the magnetic field at the centre of the solenoid. (b) Verify that if l>>a, the field tends to (B=(μ0)ni) and if a>>1, the field tends toB=((μ0)nil2a) . Interpret these results.
View Solution
Knowledge Check
A solenoid of radius R number of turn per unit length n and length L has a current I=I0cosωt. The value of induced electric field at a distance of r outside the solenoid, is :
Aμ0nI0ωR22rsinωtBμ0nI0ωR2rsinωtCμ0nI0R22rsinωtDzeroA long solenoid of radous R has n turns of wire per unit length and carries a time-varying current that varies sinusiodally as I=Imaxcosωt, where Imax is the maximum current and ω I the angular frequancy of the alternating current source (shows in Fig.)

The magnitude of the induced electric field inside tha solenoid, a distance r<R from its long central axis isA3μ0nImaxω2rsinωtBμ0nImaxω2rcosωtCμ0nImaxωrsinωtDμ0nImaxω2rsinωtA solenoid of length 0.5 m has a radius of 1 cm and is made up of 500 turns. It carries a current of 5 A. The magnetic field inside the solenoid is
A3.14×10−3TB6.28×10−3TC9.14×10−3TD1.68×10−3T
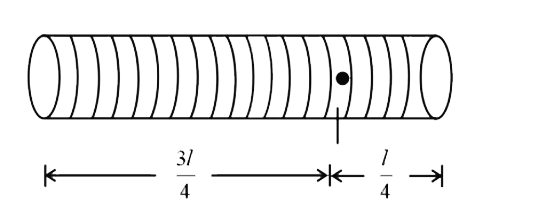
A tightly wound solenoid of radius 'a' and length 'l' has n turns per unit length. It carries an electric current i. Magnetic field at a distance l4 from one of the end (inside the solenoid on its axis) is B=μ0ni(√5+3)√K for l=4a. Then find the value of K.
View SolutionA long thin solenoid has 900tuns/metre and radius 2.50cm,. The current in the solenoid is increasing at a uniform rate of 60A/s. What is the magnitude of the induced electric field at a point?
a. 0.5cm from the axis of the solenoid.
b. 1.0cm from the axis of the solenoid.
View SolutionThe cruuent in an ideal, long solenoid is varied at a uniform rate of 0.02A/s. The solenoid has 1000 turns/s and its radius is 8 cm.
(i) Consider a circle of radius 2 cm inside the solenoid with its axis coinciding with the axis of the solenoid. Write the change in the magnetic flux through this circle in 4 s.
(ii) Find the electric field induced at a point on the circumference of the circle.
(iii) Find the electric field induced at a point outside the solenoid at a distance 9 cm from its axis.
View SolutionThe current in an ideal, long solenoid is varied at a uniform rate of 0.01As−1. The solenoid has 2000 turns/m and its radius 6.0 cm. (a) Consider a circle of radius 1.0 cm inside the solenoid with its axis coinciding with the axis of the solenoid. write the change in the magnetic flux through this circle in 2.0 seconds. (b) find the electric field induced at a point on the circumference of the circle. (c) find the electric field induced at a point outside the solenoid at a distance 8.0cm from its axis.
View SolutionA solenoid of length 2m and of radius 1 cm has a winding carrying a current of 0.1 ampere per turn. Find the magnetic field strength inside the solenoid if the total number of turns is 2000.
View Solution
