The graph between the energy of photoelectrons E and the wavelength of incident light (λ) is
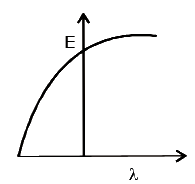
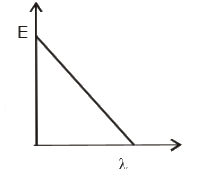
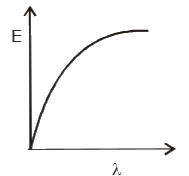

The correct Answer is:D
To solve the question regarding the graph between the energy of photoelectrons E and the wavelength of incident light λ, we will follow these steps:
Step 1: Understand the Relationship
According to Planck's quantum theory, the energy E of a photon is directly proportional to its frequency ν:
E∝ν
We can express frequency in terms of wavelength:
ν=cλ
where c is the speed of light. Thus, we can rewrite the energy equation as:
E=hν=hcλ
where h is Planck's constant.
Step 2: Analyze the Equation
From the equation E=hcλ, we can see that:
- h and c are constants.
- This implies that energy E is inversely proportional to the wavelength λ:
E∝1λ
Step 3: Determine the Graph Shape
Since E is inversely proportional to λ, we can express this relationship as:
E⋅λ=hc
This indicates that the product of energy and wavelength is a constant, which is characteristic of a hyperbolic relationship.
Step 4: Sketch the Graph
1. On the y-axis, plot the energy E.
2. On the x-axis, plot the wavelength λ.
3. As λ approaches zero, E approaches infinity. Conversely, as λ increases, E decreases.
4. The graph will be a hyperbola that approaches the axes but never touches them.
Conclusion
The graph between the energy of photoelectrons E and the wavelength of incident light λ is a hyperbola.
According to Planck's quantum theory, the energy E of a photon is directly proportional to its frequency ν:
E∝ν
We can express frequency in terms of wavelength:
ν=cλ
where c is the speed of light. Thus, we can rewrite the energy equation as:
E=hν=hcλ
where h is Planck's constant.
From the equation E=hcλ, we can see that:
- h and c are constants.
- This implies that energy E is inversely proportional to the wavelength λ:
E∝1λ
Since E is inversely proportional to λ, we can express this relationship as:
E⋅λ=hc
This indicates that the product of energy and wavelength is a constant, which is characteristic of a hyperbolic relationship.
1. On the y-axis, plot the energy E.
2. On the x-axis, plot the wavelength λ.
3. As λ approaches zero, E approaches infinity. Conversely, as λ increases, E decreases.
4. The graph will be a hyperbola that approaches the axes but never touches them.
The graph between the energy of photoelectrons E and the wavelength of incident light λ is a hyperbola.
Topper's Solved these Questions
- PHOTOELECTRIC EFFECT Book:MOTIONChapter:PHOTOELECTRIC EFFECT Exercise:EXERCISE-2 (OBJECTIVE QUESTIONS (NEET))
Explore 17 Videos
- PHOTOELECTRIC EFFECT Book:MOTIONChapter:PHOTOELECTRIC EFFECT Exercise:EXERCISE - 3 SECTION -A (Previous Year Problems (NEET ))
Explore 38 Videos
- PHOTOELECTRIC EFFECT Book:MOTIONChapter:PHOTOELECTRIC EFFECT Exercise:QUESTIONS FOR PRACTICE
Explore 12 Videos
- OPTICSBook:MOTIONChapter:OPTICSExercise:Exercise
Explore 45 Videos
- PROJECTILE MOTIONBook:MOTIONChapter:PROJECTILE MOTIONExercise:EXERCISE-3 (SECTION-B)
Explore 8 Videos
Similar Questions
Knowledge Check
The correct graph between the maximum energy of a photoelectron and the inverse of wavelength of the incident radiation is given by the curve
 AABBCCDNone of the above
AABBCCDNone of the aboveAccording to Einstein's photoelectric equation, the graph between the kinetic energy of photoelectrons ejected and the frequency of incident radiation is
A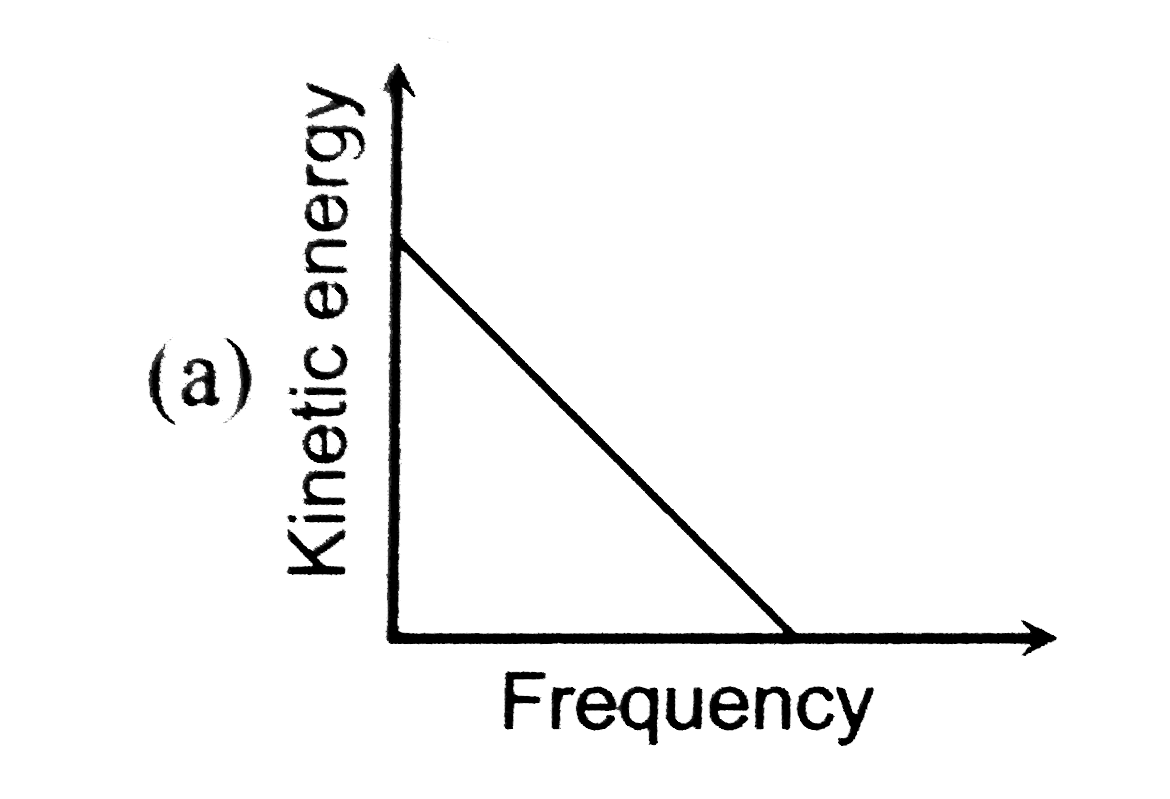 B
B C
C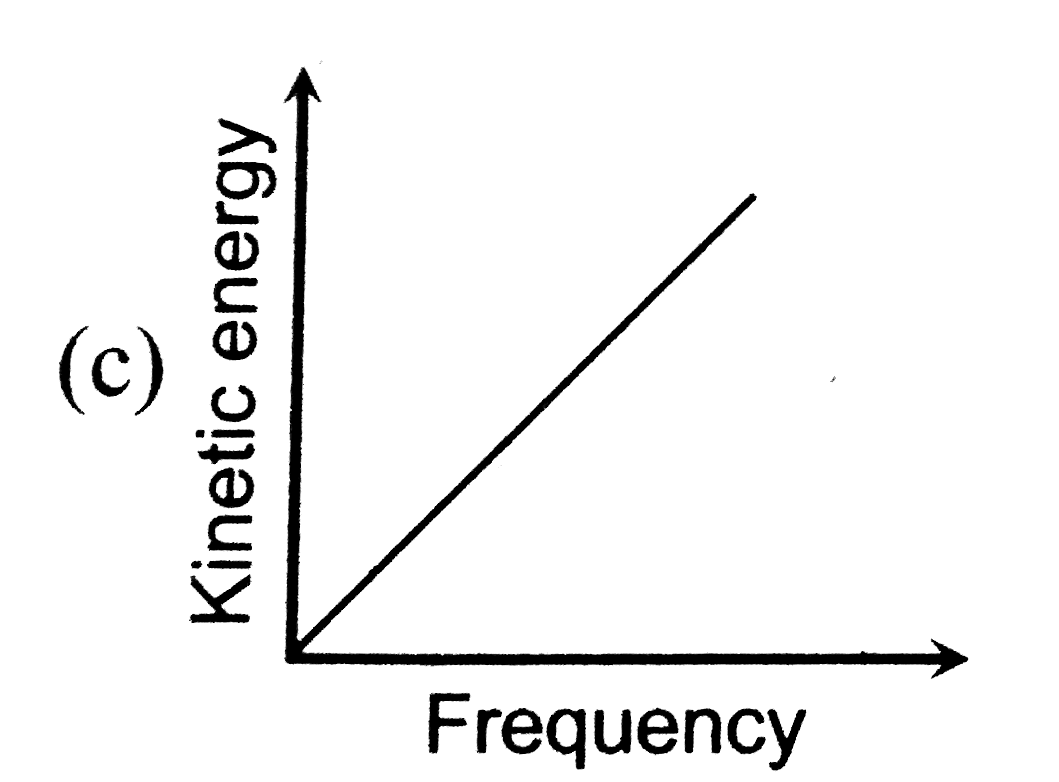 D
D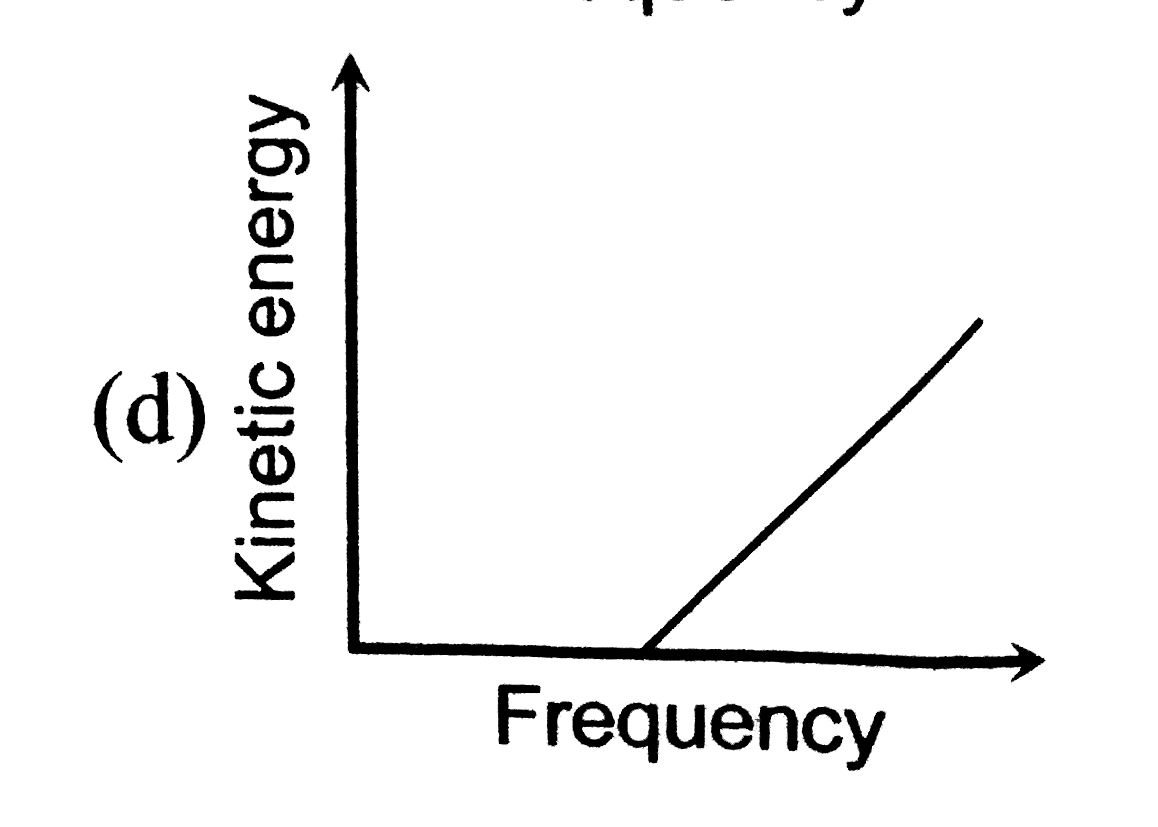
Calculate the work function of the metal, if the kinetic energies of the photoelectrons are E1 and E2, with wavelengths of incident light λ1 and λ2
AE1λ1−E2λ2λ2−λ1BE1E2λ1−λ2C(E1−E2)λ1λ2(λ1−λ2)Dλ1λ2E1(λ1−λ2)E2
What is the effect on the velocity of the emitted photoelectrons if the wavelength of the incident light is decreased ?
View SolutionMaximum kinetic energy of a photoelectron is E when the wavelength of incident light is λ. If energy becomes four times when wavelength is reduced to one thrid, then work function of the metal is
View SolutionThe correct graph respectivley the relation between energy (E) of photoelectrons and frequency v of incident light is
View SolutionAssertion : The kinetic energy of a photoelectron decrease with increases with increase in the wavelength of incident light.
Reason : All photoelectrons are not emitted with the same speed because of the range of wavelength in the white light.
View SolutionIf light of wavelength λ1 is allowed to fall on a metal , then kinetic energy of photoelectrons emitted is E1. If wavelength of light changes to λ2 then kinetic energy of electrons changes to E2. Then work function of the metal is
View Solution

