The dependence of electric potential V on the distance 'r' from the centre of a charged spherical shell is shown by :
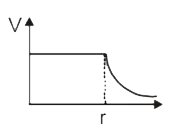
The correct Answer is:B
To solve the problem of determining the dependence of electric potential V on the distance r from the center of a charged spherical shell, we will follow these steps:
Step 1: Understand the Concept of Electric Potential
The electric potential V at a point in space due to a charge distribution is defined as the work done in bringing a unit positive charge from infinity to that point without any acceleration.
Step 2: Analyze the Electric Field Inside and Outside the Spherical Shell
For a charged spherical shell:
- Inside the shell: The electric field E is zero. Therefore, the potential V remains constant throughout the interior of the shell.
- Outside the shell: The electric field E behaves as if all the charge were concentrated at the center of the shell. The electric field at a distance r from the center (where r>R, R being the radius of the shell) is given by:
E=kQr2
where k=14πϵ0 and Q is the total charge on the shell.
Step 3: Calculate the Electric Potential Outside the Shell
Using the relation between electric field and potential:
dV=−Edr
Integrating from infinity to a point r outside the shell:
V(r)−V(∞)=−∫r∞Edr=−∫r∞kQr2dr
Calculating the integral:
V(r)−0=−(−kQr)r∞=kQr
Thus, for r>R:
V(r)=kQr
Step 4: Calculate the Electric Potential Inside the Shell
Since the electric field inside the shell is zero:
E=0⟹dV=0
Thus, the potential V inside the shell is constant and equal to the potential at the surface of the shell:
V=V(R)=kQR
Step 5: Summarize the Results
- For r<R (inside the shell):
V=kQR(constant)
- For r>R (outside the shell):
V=kQr(decreasing with increasing r)
Conclusion
The graph of V versus r will show a constant value kQR for r<R and a hyperbolic decrease for r>R. Therefore, the correct option for the dependence of electric potential V on the distance r from the center of a charged spherical shell is that V is constant inside the shell and decreases as r increases outside the shell.
The electric potential V at a point in space due to a charge distribution is defined as the work done in bringing a unit positive charge from infinity to that point without any acceleration.
For a charged spherical shell:
- Inside the shell: The electric field E is zero. Therefore, the potential V remains constant throughout the interior of the shell.
- Outside the shell: The electric field E behaves as if all the charge were concentrated at the center of the shell. The electric field at a distance r from the center (where r>R, R being the radius of the shell) is given by:
E=kQr2
where k=14πϵ0 and Q is the total charge on the shell.
Using the relation between electric field and potential:
dV=−Edr
Integrating from infinity to a point r outside the shell:
V(r)−V(∞)=−∫r∞Edr=−∫r∞kQr2dr
Calculating the integral:
V(r)−0=−(−kQr)r∞=kQr
Thus, for r>R:
V(r)=kQr
Since the electric field inside the shell is zero:
E=0⟹dV=0
Thus, the potential V inside the shell is constant and equal to the potential at the surface of the shell:
V=V(R)=kQR
- For r<R (inside the shell):
V=kQR(constant)
- For r>R (outside the shell):
V=kQr(decreasing with increasing r)
The graph of V versus r will show a constant value kQR for r<R and a hyperbolic decrease for r>R. Therefore, the correct option for the dependence of electric potential V on the distance r from the center of a charged spherical shell is that V is constant inside the shell and decreases as r increases outside the shell.
Topper's Solved these Questions
- ELECTROSTATICSBook:MOTIONChapter:ELECTROSTATICSExercise:Exercise - 2 (Objective Problems | NEET)
Explore 64 Videos
- ELECTROSTATICSBook:MOTIONChapter:ELECTROSTATICSExercise:Exercise -3 Section (A)
Explore 41 Videos
- ELECTROSTATICSBook:MOTIONChapter:ELECTROSTATICSExercise:SELF PRACTICE PROBLEM
Explore 27 Videos
- ELECTRONICS - SEMI CONDUCTORBook:MOTIONChapter:ELECTRONICS - SEMI CONDUCTORExercise:EXERCISE - 3
Explore 29 Videos
- ELECTROSTATICS - I Book:MOTIONChapter:ELECTROSTATICS - I Exercise:EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
Explore 13 Videos
Similar Questions
An isolated solid metal sphere of radius R is given an electric charge. The variation of the intensity of the electric field with the distance r from the centre of the sphere is best shown by
View SolutionWhich one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?
View Solution
Knowledge Check
The electric field at a distance 3R2 from the centre of a charged conducting spherical shell of radius R is E. The electric field at a distance R2 from the centre of the sphere is :
AEB3E2CE2DZeroThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
AE2BzeroCEDE4The electric field at a distance 3R2 from the centre of a charged conducting spherical shell of radiu R is E. The electric field at a distance R2 from the centre of the sphere is:
AzeroBECE2DE3
Two concentric spherical shells of radii r and R(r<R) have surface charge densities −σ and +σ respectively. The variation ofelectric potential V with distance x from the centre O of the shells plotted. Which of the following graphs best depict the variation qualitatively?
View SolutionA spherical shell of radius 10 cm is carrying a charge q. If the electric potential at distances 5 cm, 10 cm and 15 cm from the centre of the spherical shell is V1,V2 and V3 respectively, then
View SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R. The electric potential at the centre of the shell will be

View SolutionThe variation of electrostatic potential with radial distance r from centre of positively charged metallic thin shell of radius R is given by graph
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
View Solution

