A particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and a distance 2l apart. Prove that the motion of the particle will be SHM if it is displaced slightly along the line connecting them and released. Also find its time period.
Let the charge q at the mid-point the displaced slightly to the left.
The force on the displaced charge q due to charge q at A.
F1=14πε0q2(l+x)2

The force on the displaced charge q due to charge at B,
F2=14πε0q2(l−x)2
Net restoring force on the displaced charge q.
F=F2−F1 or F
=14πε0q2(l−x)2−14πε0q2(l+x)2
or F=q24πε0[1(l−x)2−1(l+x)2]
=q24πε04lx(l2−x2)2
Since l>>x,∴F=q2lxπε0l4 or F=q2xπε0l3
We see that F∝x and it is opposite to the direction of displacement. Therefore, the motion is SHM.
T=2π√mk, here k=q2π∈0l2
=2π√mπ∈0l2q2
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - SELF MISCELLANEOUS PROBLEM (Example )
15 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - SELF PRACTICE PROBLEM
27 Videos
- ELECTRONICS - SEMI CONDUCTORBOOK - MOTIONCHAPTER - ELECTRONICS - SEMI CONDUCTOREXERCISE - EXERCISE - 3
29 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
13 Videos
Similar Questions
A particle of mass m and charge +q is located midway between two fixed charged particles each having a charge +q and at a distance 2L apart. Assuming that the middle charge moves along the line joining the fixed charges, calculate the frequency of oscillation when it is displaced slightly.
View SolutionTwo infinitely long line charges having charge density λ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and λq>0 Neglect gravity. Find the time period.
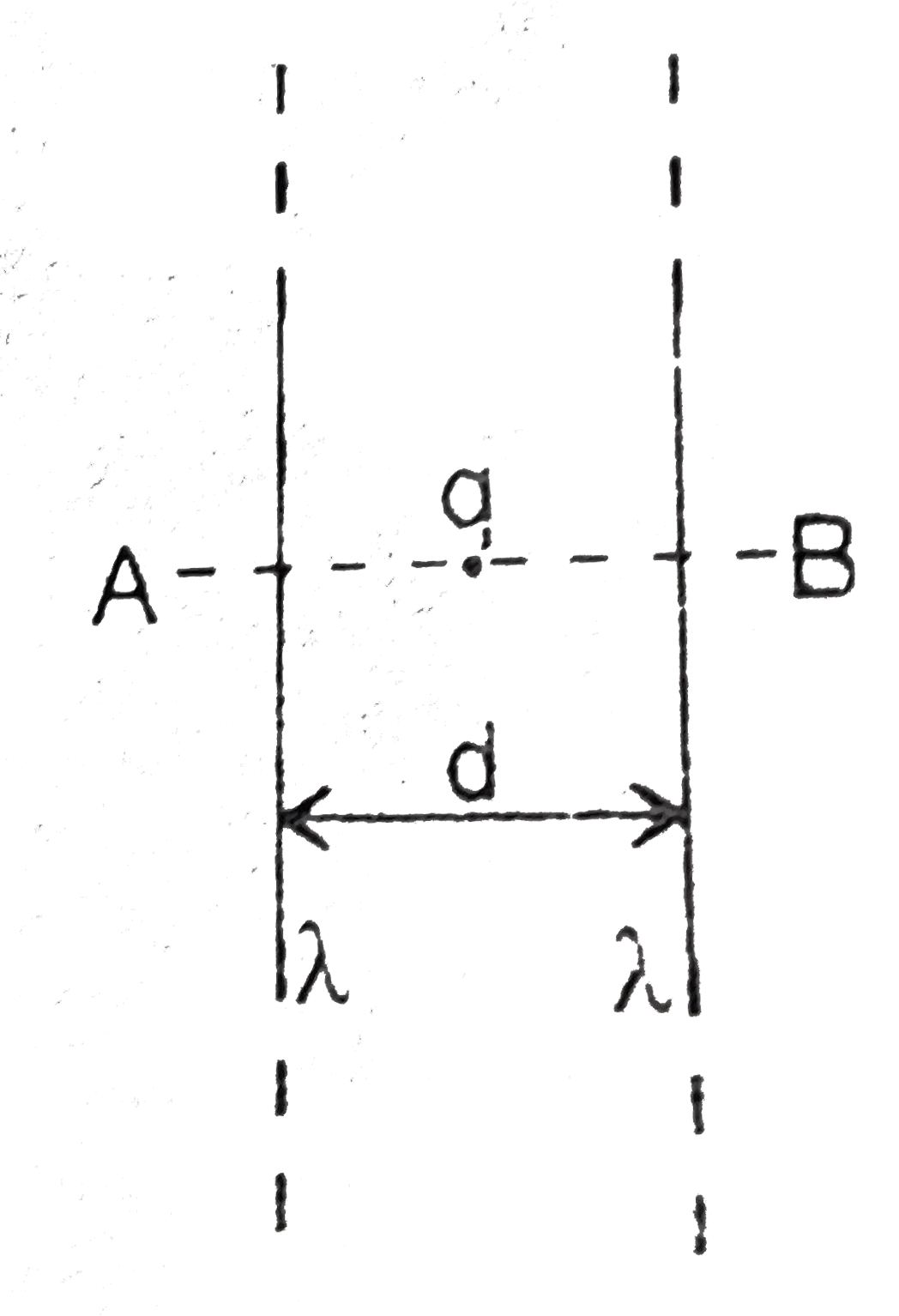
View Solution
Knowledge Check
A particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and at a distance 2L apart so that distance of this charge from each charge located at end is L. Assuming that the middle charge moves along the line joining the fixed charges. The frequency of oscillation when it is displaced slightly is
Aqπ√mπε0L3Bq4π(mπε0L3)C2qπ√mπε0L3Dq2π√mπε0L3A particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
Aq2EyBqEyCaE2yDqEy2Two positively charged particles each having charge Q and are d distance apart. A third charge is introduced in midway on the line joining the two charges. Find the nature and magnitude of third charge so that the system is in equilibrium.
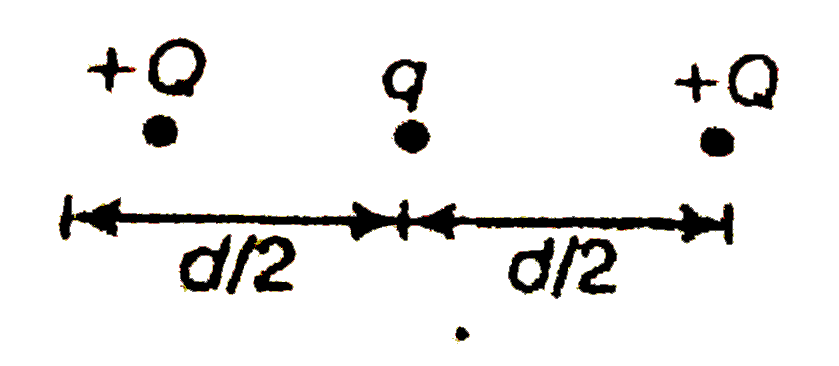 Aq=Q4Bq=Q4Cq=3Q4Dq=−3Q4
Aq=Q4Bq=Q4Cq=3Q4Dq=−3Q4
Two points charges , each Q , are fixed at separation 2d. A charged particle having charge q and mass m is placed between them.
(a) Now this charged particle is slightly displaced along the line joining the charges , slow that it will execute simple harmonic motion and find the time period of oscillation.
(b) If charge q is negative and it is displaced slightly perpendicular to the line joining the charges , repeat the part (a).
View SolutionA particle of mass m and charge -q moves along a diameter of a uniformluy charged sphere of radinus R and carrying a total charge +Q. Find the frequency of S.H.M. of the particle if the amplitude does not exceed .
View SolutionA particle of mass m carrying a charge −q1 starts moving around a fixed charge +q2 along a circulare path of radius r. Find the time period of revolution T of charge −q1.
View SolutionA thin fixed ring of radius 'R' and positive charge 'Q' is placed in a vertical plane. A particle of mass 'm' and negative charge 'q' is placed at the centre of ring. If the particle is given a small horizontal displacement, show that it executes SHM. Also find the time period of small oscillations of this particle, about the centre of ring. (Ignore gravity)
View SolutionAs shown in the adjoining figure two charge particles each having charge q and mass m and d distance apart from each other. If two particle in equilibrium under the gravitational and electric force, then determine the ratio q/m.

View Solution

