Two coils, 1 & 2, have a mutual inductance = M and resistances R each. A current flows in coil 1, which varies with time as: $I_{1} = k t^{2}$ , where K is a constant and 't' is time. Find the totalcharge that has flown through coil 2, between t=0 and t=T.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Answer

Step by step video, text & image solution for Two coils, 1 & 2, have a mutual inductance = M and resistances R each. A current flows in coil 1, which varies with time as: I_(1)=kt^(2), where K is a constant and 't' is time. Find the totalcharge that has flown through coil 2, between t=0 and t=T. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
In Fig, the mutual inductance of a coil and a very long straight wire is $M$ , coil has resistance $R$ and self-inductance $L$ . The current in the wire varies according to the law $I = a t$ , where $a$ is a constant and $t$ is the time, the time dependence of current in the coil is

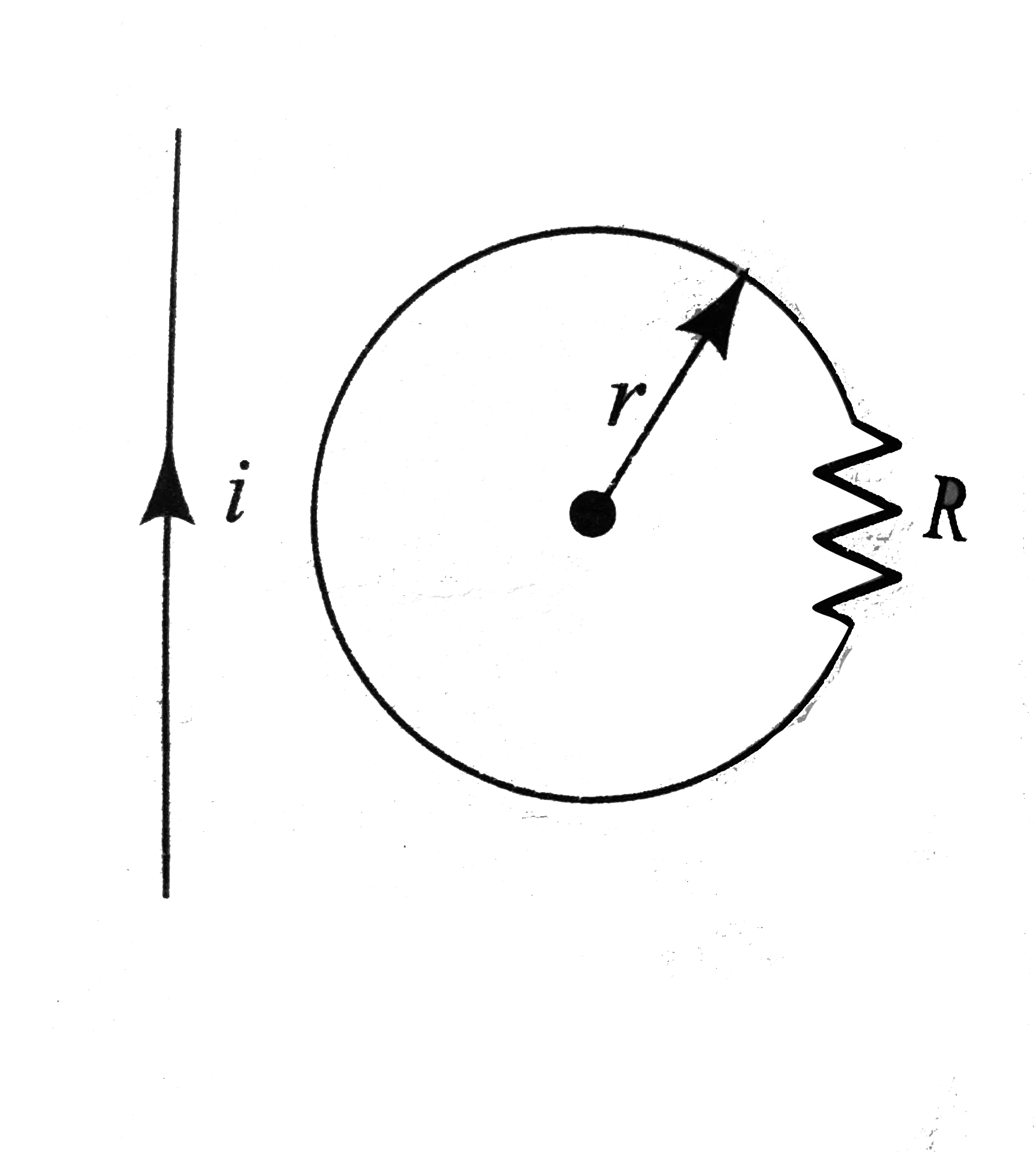A $\frac{M}{a R}$
B $m a R e^{- R t / L}$
C $\frac{M}{R} e^{- t R / L}$
D $\frac{M a}{R} (1 - e^{- t R / L})$
Question 2 - Select One
Two neighbouring coils A and B have a mutual inductance of 20 mH. The current flowing through A is given by $i = 3 t^{2} - 4 t + 6$ . The induced emf at t = 2s is
A160 mV
B200 mV
C260 mV
D300 mV
Question 3 - Select One
In the adjacent figure, the mutual inducatance of the infinite straight wire and the coil is M, while the self inductance of the coil is L. The current in infinite wire is varying according to the realtion $l_{1} = α t$ , where $α$ is a constant and $t$ is the time. The time dependence of current in the coil is

A $\frac{M α}{R}$
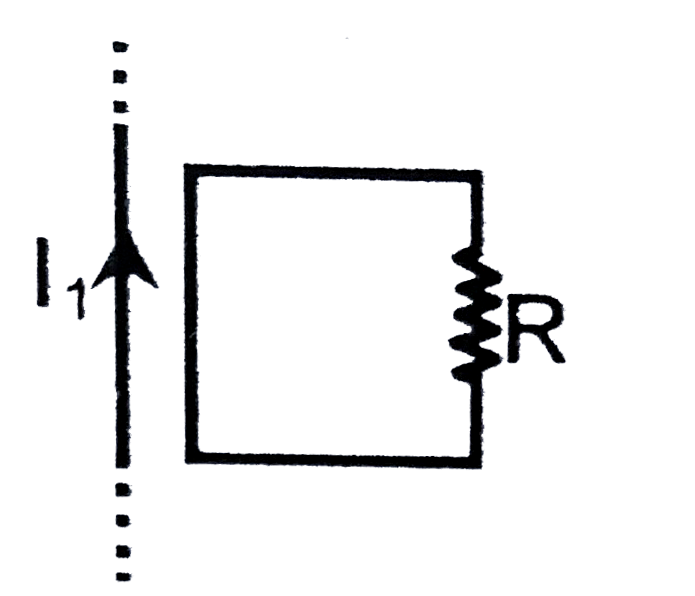B $\frac{M α L}{R} e^{- R t / L}$
C $\frac{α}{R} (1 - e^{- R t / L})$
Dnone of these

MOTION-ELECTROMAGNETIC INDUCTION-EXERCISE-3 (LEVEL-I)

Home
Ask Doubt
Profile

Two coils, 1 & 2, have a mutual inductance = M and resistances R each. A current flows in coil 1, which varies with time as: I1=kt2, where K is a constant and 't' is time. Find the totalcharge that has flown through coil 2, between t=0 and t=T.

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

In Fig, the mutual inductance of a coil and a very long straight wire is M, coil has resistance R and self-inductance L. The current in the wire varies according to the law I=at, where a is a constant and t is the time, the time dependence of current in the coil is

Two neighbouring coils A and B have a mutual inductance of 20 mH. The current flowing through A is given by i=3t2−4t+6. The induced emf at t = 2s is

MOTION-ELECTROMAGNETIC INDUCTION-EXERCISE-3 (LEVEL-I)

Two coils, 1 & 2, have a mutual inductance = M and resistances R each. A current flows in coil 1, which varies with time as: $I_{1} = k t^{2}$ , where K is a constant and 't' is time. Find the totalcharge that has flown through coil 2, between t=0 and t=T.

In Fig, the mutual inductance of a coil and a very long straight wire is $M$ , coil has resistance $R$ and self-inductance $L$ . The current in the wire varies according to the law $I = a t$ , where $a$ is a constant and $t$ is the time, the time dependence of current in the coil is

Two neighbouring coils A and B have a mutual inductance of 20 mH. The current flowing through A is given by $i = 3 t^{2} - 4 t + 6$ . The induced emf at t = 2s is