A charged ring of mass m = 50 gm, charge 2 coulomb and radius R = 2m is placed on a smooth horizontal surface. A magnetic field varying with time at a rate of (0.2 t) Tesla/sec is applied on to the ring in a direction normal to the surface of ring. Find the angular speed attained in a time t1=10sec.
The correct Answer is:A, B, C, D
To solve the problem step by step, we will follow the principles of electromagnetic induction and rotational motion.
Step 1: Understand the Given Information
- Mass of the ring, m=50g=0.05kg
- Charge on the ring, Q=2C
- Radius of the ring, R=2m
- Rate of change of magnetic field, dBdt=0.2T/s
- Time, t1=10s
Step 2: Calculate the Area of the Ring
The area A of the ring is given by the formula:
A=πR2
Substituting the value of R:
A=π(2)2=4πm2
Step 3: Calculate the Magnetic Flux
The magnetic flux Φ through the ring is given by:
Φ=B⋅A
Since B is changing with time, we can express it as:
B(t)=B0+dBdt⋅t
Assuming B0=0:
B(t)=0.2t
Thus, the magnetic flux becomes:
Φ(t)=(0.2t)⋅(4π)=0.8πtWb
Step 4: Calculate the Induced EMF
Using Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−dΦdt
Calculating the derivative:
E=−ddt(0.8πt)=−0.8πV
Step 5: Calculate the Electric Field
The electric field E induced around the ring can be calculated using:
E=E2πR
Substituting the values:
E=−0.8π2π⋅2=−0.84=−0.2V/m
Step 6: Calculate the Force on the Charge
The force F acting on the charge Q due to the electric field E is given by:
F=Q⋅E
Substituting the values:
F=2⋅(−0.2)=−0.4N
Step 7: Calculate the Torque
The torque τ acting on the ring is given by:
τ=F⋅R
Substituting the values:
τ=−0.4⋅2=−0.8N m
Step 8: Relate Torque to Angular Acceleration
Using the relation τ=I⋅α, where I is the moment of inertia of the ring:
I=mR2=0.05⋅(2)2=0.2kg m2
Thus, we have:
−0.8=0.2⋅α⟹α=−0.80.2=−4rad/s2
Step 9: Calculate the Angular Speed
The angular speed ω after time t1 can be calculated using:
ω=ω0+αt1
Assuming the initial angular speed ω0=0:
ω=0+(−4)(10)=−40rad/s
Since we are interested in the magnitude, we take:
ω=40rad/s
Final Answer
The angular speed attained in a time t1=10s is:
ω=40rad/s
- Mass of the ring, m=50g=0.05kg
- Charge on the ring, Q=2C
- Radius of the ring, R=2m
- Rate of change of magnetic field, dBdt=0.2T/s
- Time, t1=10s
The area A of the ring is given by the formula:
A=πR2
Substituting the value of R:
A=π(2)2=4πm2
The magnetic flux Φ through the ring is given by:
Φ=B⋅A
Since B is changing with time, we can express it as:
B(t)=B0+dBdt⋅t
Assuming B0=0:
B(t)=0.2t
Thus, the magnetic flux becomes:
Φ(t)=(0.2t)⋅(4π)=0.8πtWb
Using Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−dΦdt
Calculating the derivative:
E=−ddt(0.8πt)=−0.8πV
The electric field E induced around the ring can be calculated using:
E=E2πR
Substituting the values:
E=−0.8π2π⋅2=−0.84=−0.2V/m
The force F acting on the charge Q due to the electric field E is given by:
F=Q⋅E
Substituting the values:
F=2⋅(−0.2)=−0.4N
The torque τ acting on the ring is given by:
τ=F⋅R
Substituting the values:
τ=−0.4⋅2=−0.8N m
Using the relation τ=I⋅α, where I is the moment of inertia of the ring:
I=mR2=0.05⋅(2)2=0.2kg m2
Thus, we have:
−0.8=0.2⋅α⟹α=−0.80.2=−4rad/s2
The angular speed ω after time t1 can be calculated using:
ω=ω0+αt1
Assuming the initial angular speed ω0=0:
ω=0+(−4)(10)=−40rad/s
Since we are interested in the magnitude, we take:
ω=40rad/s
The angular speed attained in a time t1=10s is:
ω=40rad/s
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:MOTIONChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE-3 (LEVEL-II)
Explore 3 Videos
- ELECTROMAGNETIC INDUCTIONBook:MOTIONChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE-4 (LEVEL-I)
Explore 11 Videos
- ELECTROMAGNETIC INDUCTIONBook:MOTIONChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE-2 (LEVEL-II)
Explore 2 Videos
- ELECTRO MAGNETIC WAVES Book:MOTIONChapter:ELECTRO MAGNETIC WAVES Exercise:EXERCISE - 3 (SECTION - B)
Explore 8 Videos
- ELECTROMAGNETISMBook:MOTIONChapter:ELECTROMAGNETISMExercise:Exercise
Explore 136 Videos
Similar Questions
A metal rign of mass m and radius R is placed on a smooth horizontal table and is set rotating abut its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
View SolutionA conducting ring of mass 2 kg and radius 0.5 m is placed on a smooth horizontal plane. The ring carries a current 4A . A horizontal magnetic field B = 10T is switched on at time t = 0 as shown in figure. The initial angular acceleration of the ring will be:

View Solution
Knowledge Check
A hollow cylinder of mass m and radius r is kept on a smooth horizontal surface. Horizontal force F is applied at a height above the centre. Find the value of h/R so that ring performs pure rolling on the surface.
A1B12C13D25There is a non conducting ring of radius R and mass m having charge q uniformly distributed over its circumference. It is placed on a rough horizontal surface. A vertical time varying uniform magnetic field B=4t2 is switched on at time t= 0. The coefficient of friction between the ring and the table, if the ring starts rotating at t= 1 sec, is :
A4qMRgB4qRmgC8qRmgDqR2mgA conducting rign of mass 100 gram and radius 0⋅5m is placed on a smooth horizontal plane. The ring carries a current of I=4A. A horizontal magnetic field B=10T is switched on at time t=0 as shown in figure. The initial angular acceleration of the ring is
 A200πrad/s2B400πrad/s2C800πrad/s2D1200πrad/s2
A200πrad/s2B400πrad/s2C800πrad/s2D1200πrad/s2
Ring of mass M and radius 1m placed on smooth horizontal surface at rest. A particle of same mass M moving horizontally with speed 6m/s strike the ring and stick to it as shown in figure. Find angular speed of system after collision in rad/sec.

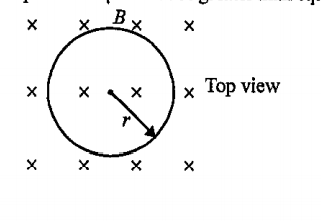
View SolutionA nonconducting ring (of mass m, radius r, having charge Q) is placed on a rough horizontal surface (in a cylindrical region with transverse magnetic field). The field is increasing with time at the rate R and coefficient of friction between the surface and the ring is μ. For ring to remain in equilibrium μ should be greater than equal to,
View SolutionA ring of mass m and radius R is placed on a rough horizontal surface (co-efficient of friction μ) with velocity of C.M.v0 and angular speed 2V0R as shown in figure. Initially the ring is rolling with slipping but attains pure rolling motion after some time t. Then
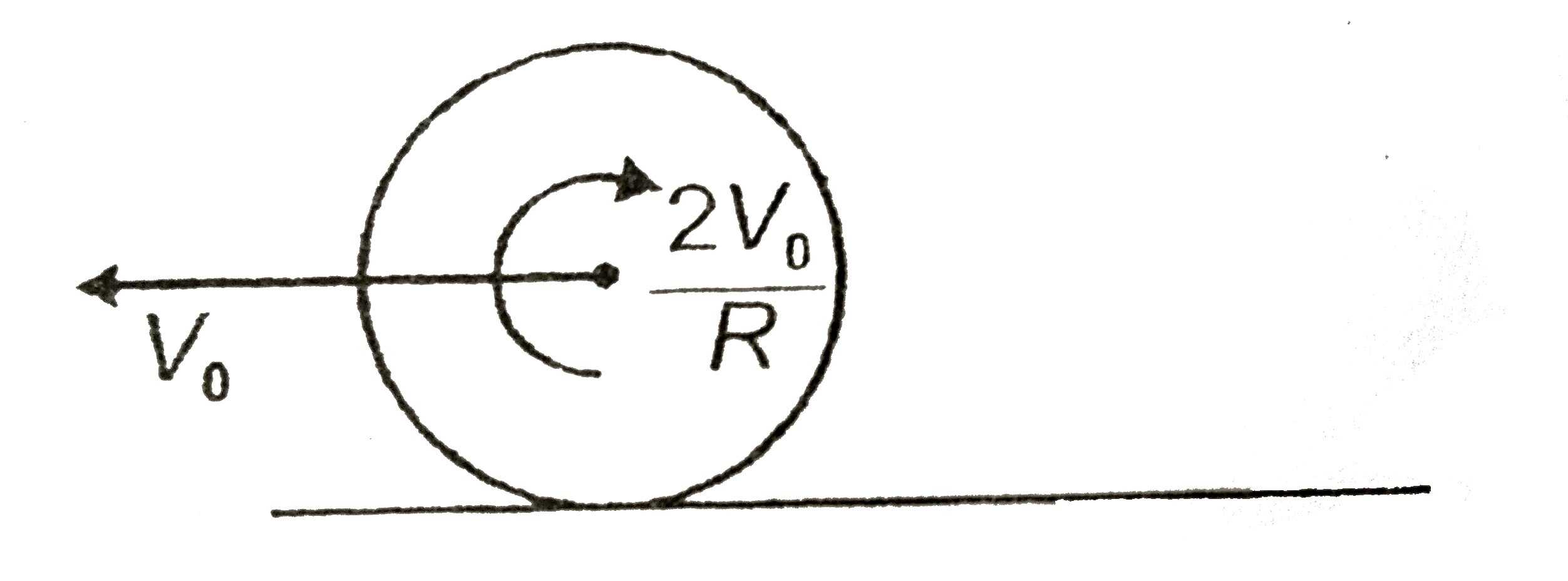
View SolutionA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

View SolutionA conducting ring of mass 2kg and radius 0.5m is placed on a smooth plane. The ring carries a current of i=4A. A horizontal magnetic field B=10T is switched on at time t=0 as shown in fig The initial angular acceleration of the ring will be
 .
.
View Solution

