Two parallel, long, straight conductors lie on a smooth plane surface. Two other parallel conductors rest on them at right angles so as to form a square of side a initially. A uniform magnetic field B exists at right angles to the plane containing the conductors. Now they start moving out with a constant velocity (v).
Will the induced emf be time dependent?
To determine whether the induced emf in the given scenario is time-dependent, we can follow these steps:
Step 1: Understand the setup
We have two pairs of parallel conductors forming a square of side length a. A uniform magnetic field B is present perpendicular to the plane of the conductors. When the conductors start moving with a constant velocity v, we need to analyze how this motion affects the magnetic flux through the square formed by the conductors.
Hint: Visualize the arrangement of the conductors and the magnetic field to understand how they interact.
Step 2: Analyze the magnetic flux
The magnetic flux Φ through the square formed by the conductors is given by:
Φ=B×A
where A is the area of the square. Initially, the area A is a2.
Hint: Remember that the area of the square will change as the conductors move.
Step 3: Determine how the area changes
As the conductors move outward with a velocity v, the length of each side of the square increases. After a time t, the new length of each side becomes:
a+vt
Thus, the new area A becomes:
A=(a+vt)2
Hint: Consider how the area changes as the conductors move apart.
Step 4: Calculate the new magnetic flux
Now, substituting the new area into the magnetic flux equation:
Φ(t)=B×(a+vt)2
Hint: This expression shows that the magnetic flux is a function of time due to the term vt.
Step 5: Find the induced emf
According to Faraday's law of electromagnetic induction, the induced emf E is given by:
E=−dΦdt
Calculating the derivative, we have:
E=−ddt(B(a+vt)2)=−B⋅2(a+vt)⋅v
This indicates that the induced emf depends on time through the term vt.
Hint: Differentiate the expression for flux with respect to time to find the induced emf.
Step 6: Conclusion
Since the induced emf E is a function of time (specifically, it includes the term vt), we conclude that the induced emf is indeed time-dependent.
Final Answer: Yes, the induced emf is time-dependent.
We have two pairs of parallel conductors forming a square of side length a. A uniform magnetic field B is present perpendicular to the plane of the conductors. When the conductors start moving with a constant velocity v, we need to analyze how this motion affects the magnetic flux through the square formed by the conductors.
The magnetic flux Φ through the square formed by the conductors is given by:
Φ=B×A
where A is the area of the square. Initially, the area A is a2.
As the conductors move outward with a velocity v, the length of each side of the square increases. After a time t, the new length of each side becomes:
a+vt
Thus, the new area A becomes:
A=(a+vt)2
Now, substituting the new area into the magnetic flux equation:
Φ(t)=B×(a+vt)2
According to Faraday's law of electromagnetic induction, the induced emf E is given by:
E=−dΦdt
Calculating the derivative, we have:
E=−ddt(B(a+vt)2)=−B⋅2(a+vt)⋅v
This indicates that the induced emf depends on time through the term vt.
Since the induced emf E is a function of time (specifically, it includes the term vt), we conclude that the induced emf is indeed time-dependent.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MOTIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-1
25 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MOTIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-2 (LEVEL-I)
16 Videos
- ELECTRO MAGNETIC WAVES BOOK - MOTIONCHAPTER - ELECTRO MAGNETIC WAVES EXERCISE - EXERCISE - 3 (SECTION - B)
8 Videos
- ELECTROMAGNETISMBOOK - MOTIONCHAPTER - ELECTROMAGNETISMEXERCISE - Exercise
136 Videos
Similar Questions
Two parallel, long, straight conductors lie on a smooth plane surface. Two other parallel conductors rest on them at right angles so as to form a square of side a initially. A uniform magnetic field B exists at right angles to the plane containing the conductors. Now they start moving out with a constant velocity (v).
Will the current be time dependent?
View SolutionTwo parallel, long, straight conductor lie on a smooth plane surface. Two other parallel so as to form a square of side a initially. A uniform magnetic field B exists at right angles to the plane containing the cinductors. Now they start moving out with a constant velocity v.
(A) Will the induced emf be time dependent?
(b) Will the current be time dependent ?
View Solution
Knowledge Check
Two parallel long straight conductors lie on a smooth surface. Two other parallel conductors rest on them at right angless so as to form a square of side a initially. A uniform magnetic field B exists at right angles to the plane containing the conductors. They all start moving out with a constant velocity v. If r is the resistance per unit length of the wire the current in the circuit will be
ABvrBBrvCBvrDBvTwo parallel long straight conductors lie on a smooth plane surface. Two other parallel conductors rest on them at right angle so as to form a square of side a. A uniform magnetic field B exists at right angle to the plane containing the conductors. Now, conductors starts moving outward with a constant velocity v0 at t=0. Then, induced current in the loop at any time is (λ is resistance per unit length of the conductors)
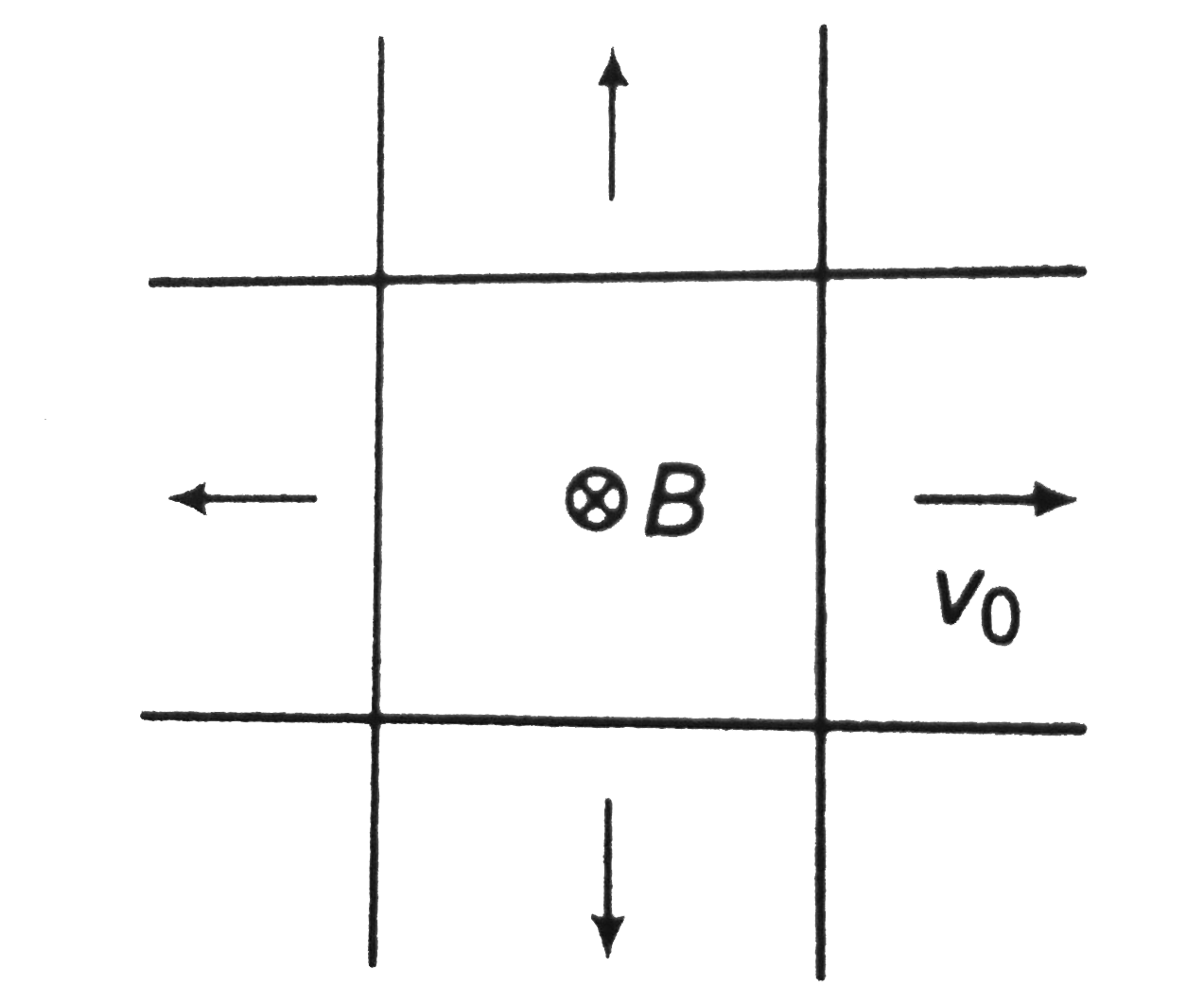AaBv0λ(a+v0t)BaBv02λCBv0λDBv02λTwo parallel long straight conductors lie on a smooth horizontal surface. Two other parallel conductor rest on them at right angles so as from B exits vertical. A uniform magnetic field B exists a vertical direction. Now all the four conductors stock moving outwards with a constant velocity v. The induced emf e and induced current i will vary wide time t as
A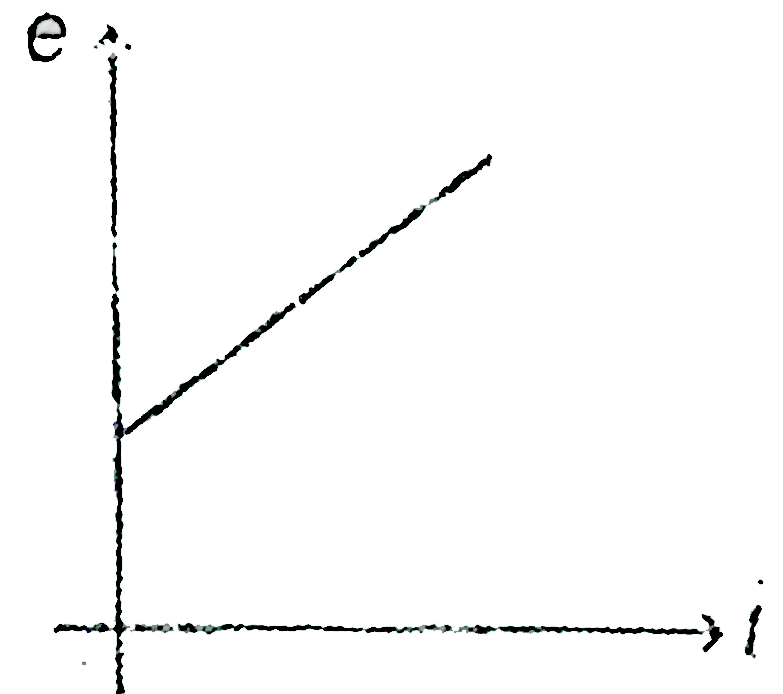
B
C
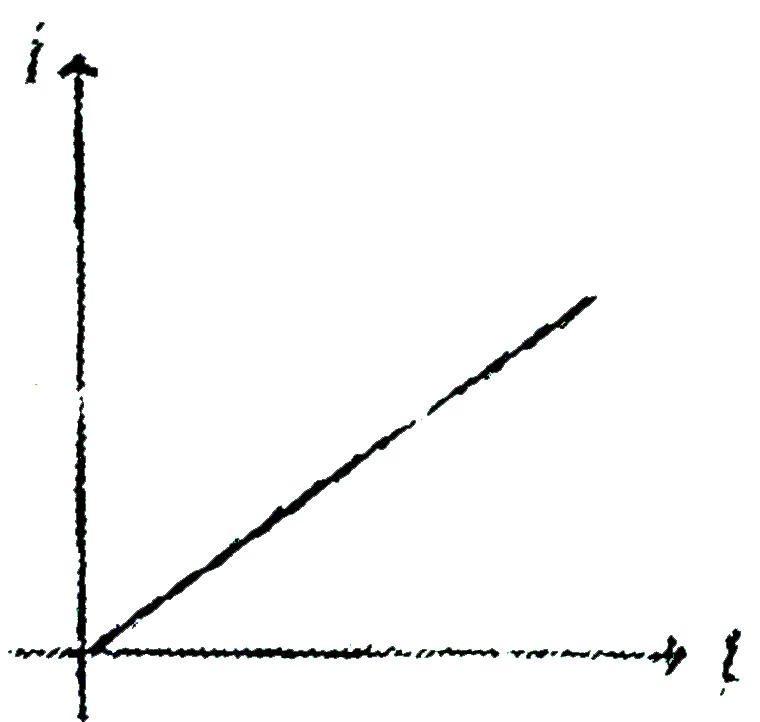D
An electron and a proton moving parallel to each other in the same direction with equal momentra, enter into a uniform magnetic field which is at right angles to their velocities. Trace their trajectories in the magnetic field.
View SolutionA straight conductor 1 meter long moves a right angles to both, its length and a uniform magnetic field. If the speed of the conductor is 2.0ms−1 and the strength of the magnetic field is 104 gauss, find the value of induced emf in volt.
View SolutionA square conducting loop of side L and resistance R is moving with a uniform velocity at right angles to one of the side in its own plane . On applying a uniform magnetic field at right angles to its plane as show in the figure the induced current in the loop will be __
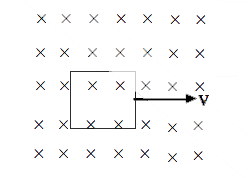
View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
View SolutionTwo parallel fixed conducting rails are l distance apart. They are connected by a conducting wire xy. A uniform magnetic field B is applied normal to its plane. Two other rods PQ and RT(RS = ST) are moved with a constant velocity v. Resistance/ length of these two rods are λ no other wire has resistance. Then :
View Solution