Two circular loops of equal radii are placed, one vertically and other horizontally with a common center. The current flowing is clock-wise in both and has same magnitude. The direction of magnetic field at the center :
To solve the problem of determining the direction of the magnetic field at the center of two circular loops (one vertical and one horizontal) with a common center and current flowing clockwise in both, we can follow these steps:
1. Identify the Configuration:
- We have two circular loops of equal radii.
- One loop is oriented vertically, and the other is oriented horizontally.
- Both loops have a common center.
2. Determine the Direction of Magnetic Field from Each Loop:
- For the horizontal loop:
- The current flows clockwise when viewed from above.
- According to the right-hand rule, if you curl your fingers in the direction of the current (clockwise), your thumb points downward.
- Therefore, the magnetic field at the center due to the horizontal loop is directed downward.
- For the vertical loop:
- The current also flows clockwise when viewed from the side (the same perspective as the horizontal loop).
- Applying the right-hand rule again, curling your fingers in the direction of the current (clockwise) will have your thumb pointing towards the left.
- Thus, the magnetic field at the center due to the vertical loop is directed to the left.
3. Combine the Magnetic Fields:
- We have two magnetic fields at the center:
- One directed downward (from the horizontal loop).
- One directed to the left (from the vertical loop).
- Since both magnetic fields are equal in magnitude and perpendicular to each other, we can use vector addition to find the resultant magnetic field.
4. Calculate the Resultant Magnetic Field:
- The magnitude of the resultant magnetic field Bresultant can be calculated using the Pythagorean theorem:
Bresultant=√B2+B2=√2B2=B√2
- The direction of the resultant magnetic field can be found using trigonometry. The angle θ with respect to the downward direction can be calculated as:
tan(θ)=BleftBdown=BB=1⟹θ=45∘
5. Conclusion:
- The resultant magnetic field at the center of the loops is directed at an angle of 45∘ from the downward direction towards the left.
Final Answer:
The direction of the magnetic field at the center is at an angle of 45∘ from the downward direction towards the left.
- We have two circular loops of equal radii.
- One loop is oriented vertically, and the other is oriented horizontally.
- Both loops have a common center.
- For the horizontal loop:
- The current flows clockwise when viewed from above.
- According to the right-hand rule, if you curl your fingers in the direction of the current (clockwise), your thumb points downward.
- Therefore, the magnetic field at the center due to the horizontal loop is directed downward.
- The current also flows clockwise when viewed from the side (the same perspective as the horizontal loop).
- Applying the right-hand rule again, curling your fingers in the direction of the current (clockwise) will have your thumb pointing towards the left.
- Thus, the magnetic field at the center due to the vertical loop is directed to the left.
- We have two magnetic fields at the center:
- One directed downward (from the horizontal loop).
- One directed to the left (from the vertical loop).
- Since both magnetic fields are equal in magnitude and perpendicular to each other, we can use vector addition to find the resultant magnetic field.
- The magnitude of the resultant magnetic field Bresultant can be calculated using the Pythagorean theorem:
Bresultant=√B2+B2=√2B2=B√2
- The direction of the resultant magnetic field can be found using trigonometry. The angle θ with respect to the downward direction can be calculated as:
tan(θ)=BleftBdown=BB=1⟹θ=45∘
- The resultant magnetic field at the center of the loops is directed at an angle of 45∘ from the downward direction towards the left.
The direction of the magnetic field at the center is at an angle of 45∘ from the downward direction towards the left.
Topper's Solved these Questions
- MAGNETISM Book:MOTIONChapter:MAGNETISM Exercise:EXERCISE-3 (Level-II)
Explore 23 Videos
- MAGNETISM Book:MOTIONChapter:MAGNETISM Exercise:EXERCISE-4 (LEVEL-I)
Explore 33 Videos
- MAGNETISM Book:MOTIONChapter:MAGNETISM Exercise:EXERCISE-2 (Level-II)
Explore 15 Videos
- LOGIC GATESBook:MOTIONChapter:LOGIC GATESExercise:EXERCISE - 2
Explore 10 Videos
- MAGNETISM -1Book:MOTIONChapter:MAGNETISM -1Exercise:Exercise - 3 SECTION -A
Explore 56 Videos
Similar Questions
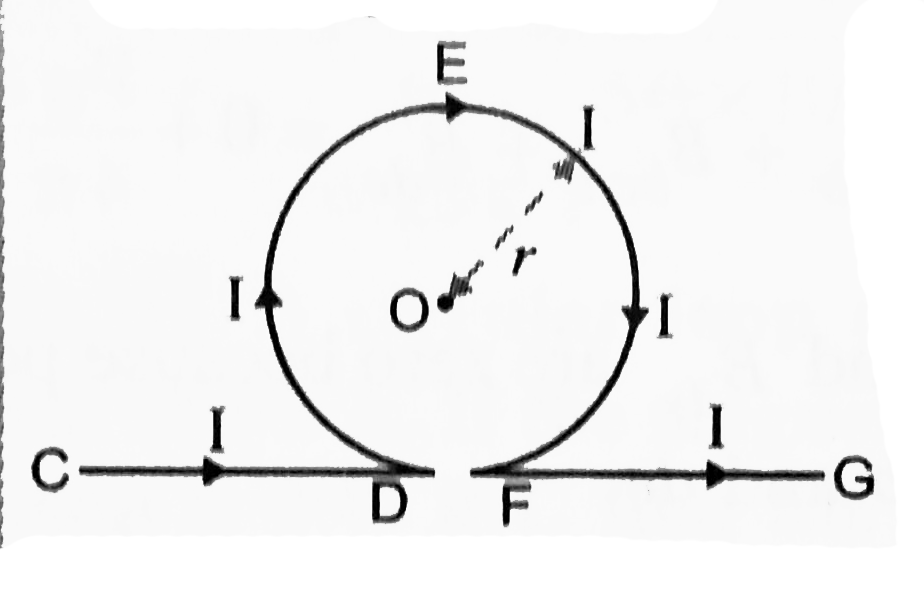
If a long horizontal conductor is bent as shown in figure and a current I is passed in it, find the magnitude and direction of magnetic field induction at the centre of circular part.
View SolutionThe plane of a circular coil is horizontal. It has 10 turns each of radius 8cm. A current of 2 A flows through it. The current appears to flow clockwise from a point above the coil. Find the magnitude and direction of magnetic field at the centre of the coil due to the current.
View Solution
Knowledge Check
Two circular loops P and Q are placed with their planes paraller to each other. A current is flowing through P . If this current is increasesed, then
 Athe loop will attract each otherBthe loops will repel each otherCthe loops will neither attract nor repel each otherDloop Q will strat rotating
Athe loop will attract each otherBthe loops will repel each otherCthe loops will neither attract nor repel each otherDloop Q will strat rotatingA wire in the from of a circular loop of one turn carrying a current produces a magnetic fild B at the centre. If the same wire is looped into a coil of two turns and carreis the same current, the new value of magnetic induction at the centre is
A5BB3BC2BD4B
(a) Draw the pattern of magnetic field lines for a circular coil carrying current.
(b) Two identical planes such that they have a common centre at P as shown in the figure. Find the magnitude and direction of the net magnetic field at the point P due to the loops
View SolutionTwo small circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in figure. Find the magnitude and direction of the net magnetic field produced at the point O.
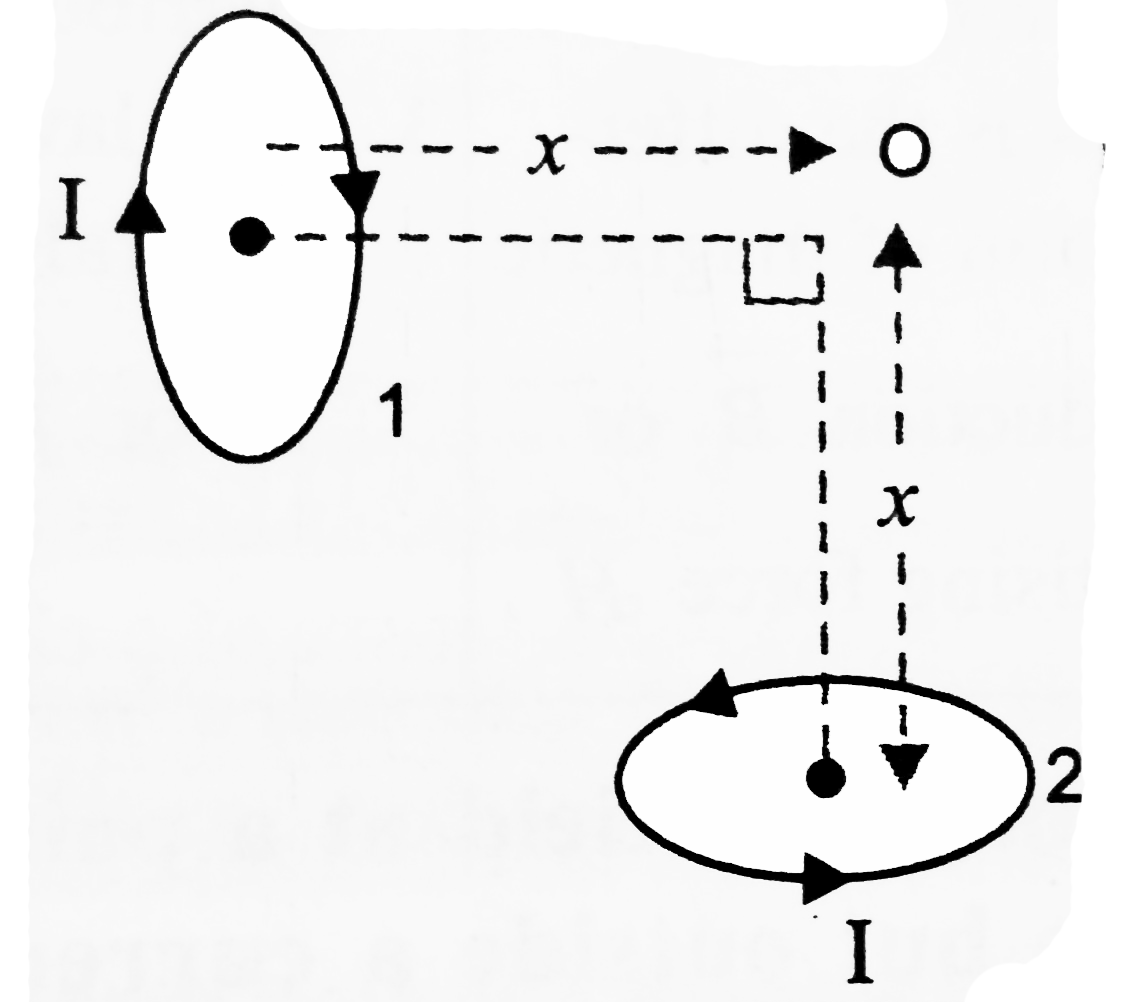
View SolutionA Helmholtz coil has a pair of loops, each withN turns and radius R. They are placed coaxially at distance R and the same current I flows through the loops in the same direction. The magnitude of magnetic field at P, midway between the centres A and C, is given by [Refer to figure given below]:

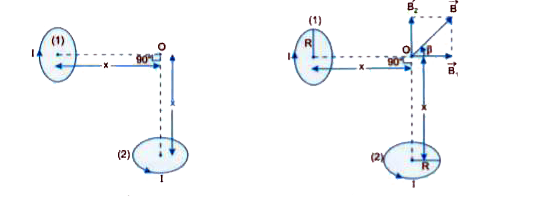
View SolutionTwo small identical circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in the fig. Find the fig. Find the magnitude and direction of the net magnetic field at the net magnetic field at the point O.
View SolutionTwo circular coils, each of 100 turns, are held that one lies in the vertical plane and the other in the horizontal plane with their centres coinciding. The radii of the vertical and the horizontal coils are respectively 20 cm and 30 cm. If the directions of the currents in them are such that the earth's magnetic field at the centre of the coils is exactly neutralised, then calculate the current in each coil. (Horizontal component of earth's magnetic field=27.8Am−1, angle of dip=30∘
View SolutionTwo circular loops of equal radii are placed coaxially at some separation. The first is cut and a battery is inserted in between to drive a current in it. The current changes slightly because of the variation in resistance with temperature. During this period, the two loops
View Solution

