Six wires of current I1=1A,I2=2A,I3=3A,I4=1A,I5=5A and I6=4A cut the page perpendicularly at the points 1,2,3,4,5 and 6 respectively as shown in the figure
Find the value of the integral ∮→B.−→d1 around the closed path

m0 weber. m1
Topper's Solved these Questions
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-3 (Level-II)
23 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-4 (LEVEL-I)
33 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-2 (Level-II)
15 Videos
- LOGIC GATESBOOK - MOTIONCHAPTER - LOGIC GATESEXERCISE - EXERCISE - 2
10 Videos
- MAGNETISM -1BOOK - MOTIONCHAPTER - MAGNETISM -1EXERCISE - Exercise - 3 SECTION -A
56 Videos
Similar Questions
Knowledge Check
Six wires of current I1=1A,I2=2A,I3=3A,I4=1A,I5=4AandI6=5A, cut the page perpendicularly at points 1, 2, 3, 4, 5 and 6. The value of line integral of B around the dotted closed path (i.e. o∫→B.d→l) is
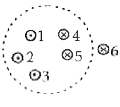 AzeroBμ0Wbm−1C2μ0Wbm−1D4μ0Wbm−1
AzeroBμ0Wbm−1C2μ0Wbm−1D4μ0Wbm−1
Find relation in between current i1,i2,i3,i4,i5 and i6.
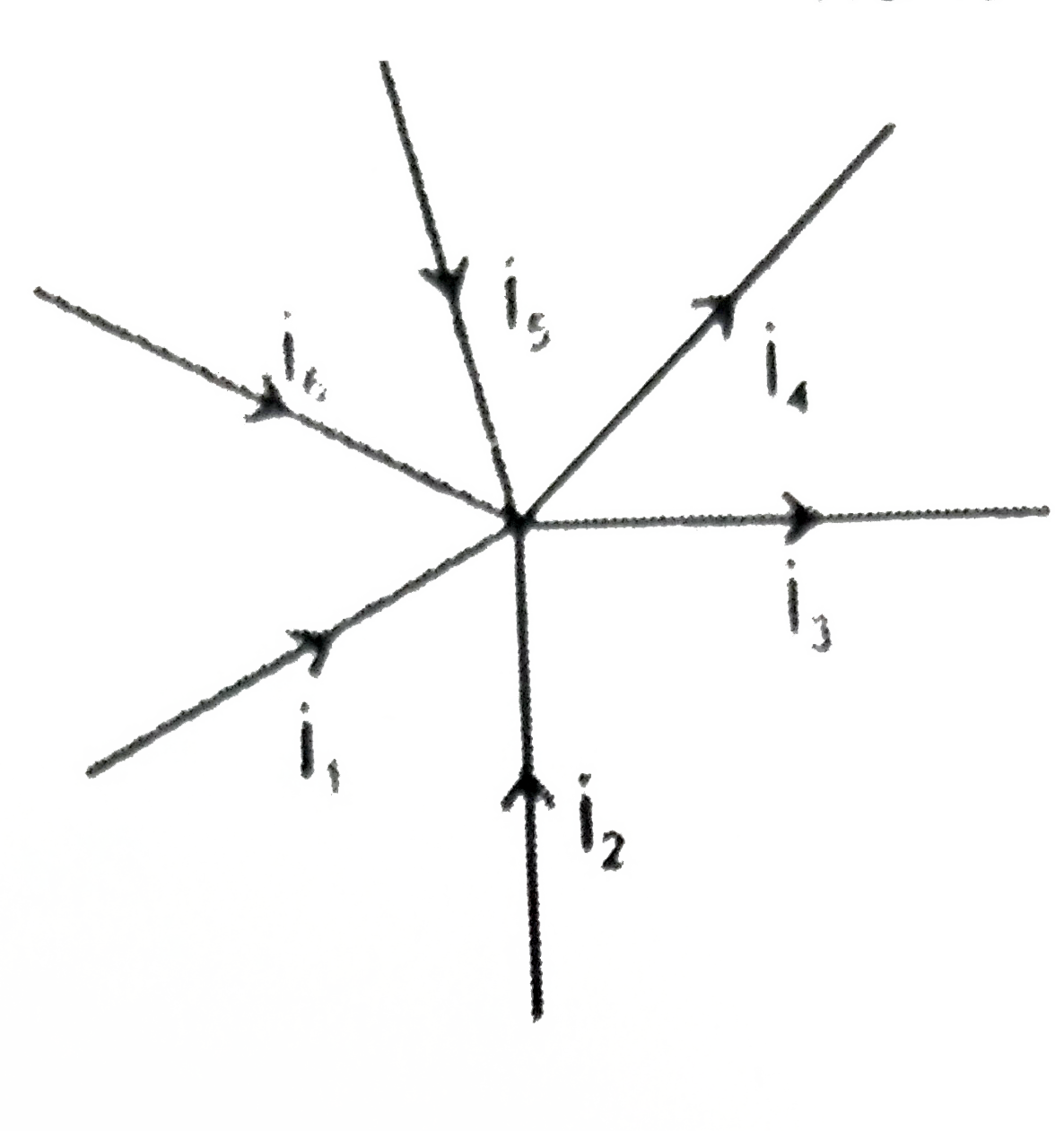
View Solutionfind the value of |3+4i|+|1+5i|2
View SolutionIn the given circuit diagram, the currents, I1=−0.34,I4=0.8A, and I5=0.4A, are flowing as shown. The currents I2,I3 and I6, respectively, are :
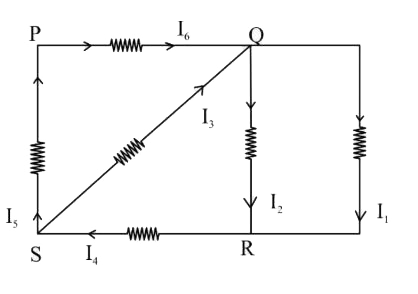
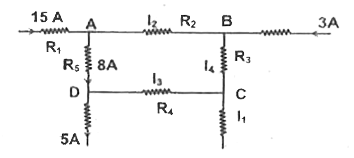
View SolutionCalculate the values of currents I1,I2,I3,andI4 in the section of networks shown in Fig 5.64

View SolutionCalculate the values of currents ·I1I2I3andI4 Is and loin the section of networks shown in the figure
View SolutionConsider a uniform square plate shown in the figure. I1,I2,I3 and I4 are moment of inertia of the plate about the axes 1, 2, 3 and 4 respectively. Axes 1 and 2 are diagonals and 3 and 4 are lines passing through centre parallel to sides of the square. The moment of inertia of the plate about an axis passing through centre and perpendicular to the plane of the figure is equal to which of the followings.
(a) I3+I4
(b) I1+I3
(c) I2+I3
(d) 12(I1+I2+I3+I4)
View SolutionThe figure shows three straight current carrying conductors having current I1,I2 and I3 respectively. Calculate line integral of magnetic induction field →B along the closed path ABCDEFA

View Solution
