Velocity of water in a river is
As velocity at the bottom of the river will be zero, velocity gradient,
dvdy=18×10360×60×15=1s−1
Now as the viscous force F=ηA(dv/dy) is tangential to the area, Shear stress =F11A=ηdvdy
=10−3×1=1×10−3N/m2
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - SURFACE TENSION & VISCOSITY EXERCISE - Exercise - 1 Objective Problems | JEE Main19videos
SURFACE TENSION & VISCOSITY
- BOOK - MOTIONCHAPTER - SURFACE TENSION & VISCOSITY EXERCISE - Exercise - 2 (Level-I) Objective Problems | JEE Main11videos
SURFACE TENSION & VISCOSITY
- BOOK - MOTIONCHAPTER - SURFACE TENSIONEXERCISE - Exercise - 3 | Section - B Previous Year Problems | AIEEE12videos
SURFACE TENSION
- BOOK - MOTIONCHAPTER - ThermodynamicsEXERCISE - EXERCISE - 3 SECTION b26videos
Thermodynamics
Similar Questions
Give reason for the following:
(a) Machine parts get jammed in the winters.
(b) A constant driving force is always required for the maintenance of the flow of oil through pipe lines in the refineries.
(c) Velocity of water in a river is less near the banks and more in the middle.View SolutionThe velocity of water near a river's surface is 20 km/hr. If the depth of the river is 4 m, calculate the shearing stress between the horizontal layers of water. Take, coefficient of viscosity of water = 0.01 poise.
View Solution
Knowledge Check
- Question 1 - Select One
The velocity of water in river is 9 km/h of the upper surface . The river is 10 m deep . If the coefficient of viscosity of water is 10−2 poise then the shearing stress between horizontal layers of water is
A0.25×10−2N/m2B0.25×10−3N/m2C0.5×10−3N/m2D0.75×10−3N/m2 - Question 2 - Select One
The velocity of water in river is 180 km h−1 near the surface .If the river is 5 m deep, then the shearing stress between the surface layer and the bottom layer is ( coefficient of viscosity of water η=10−3 Pa s)
A10−2Nm−2B10−3Nm−2C10−4Nm−2D10−5Nm−2 - Question 3 - Select One
A person reaches on a point directly opposite on the other bank of a river.The velocity of the water in the river is 4m/sand the velocity of the person in still water is 5m/s.If the width of the river is 84.6m, time taken to cross the river in seconds is
A9.4B2C84.6D28.2
The velocity if a swimmer (v) in stil water is less than the velocity of water (u) in a river. Show that the swimmer must aim himself at an angles cos−1 (v/u) with upstream in order to cross the river along the shortest possible path. Find thr drifting (distance moved along the direction of stream in crossing the river) of the swimmer along this shortest possible path.
View SolutionVelocity of man w.r.t river is equal to velocity at river value of θ for which man reaches directly at B
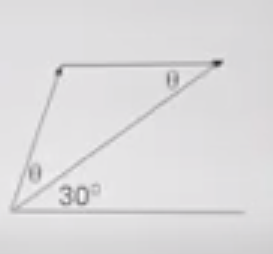 View Solution
View SolutionA swimmer crosses the river along the line making an angle of 45∘ with the direction of flow. Velocity of the river is 5 m/s. Swimmer takes 6 seconds to cross the river of width 60 m. The velocity of the swimmer with respect to water will be :
View SolutionA swimmer crosses the river along the line making an angle of 45∘ with the direction of flow. Velocity of the river water is 5ms. Swimmer takes 12 seconds to cross the river of width 60 m. The velocity of the swimmer with respect to water will be:
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
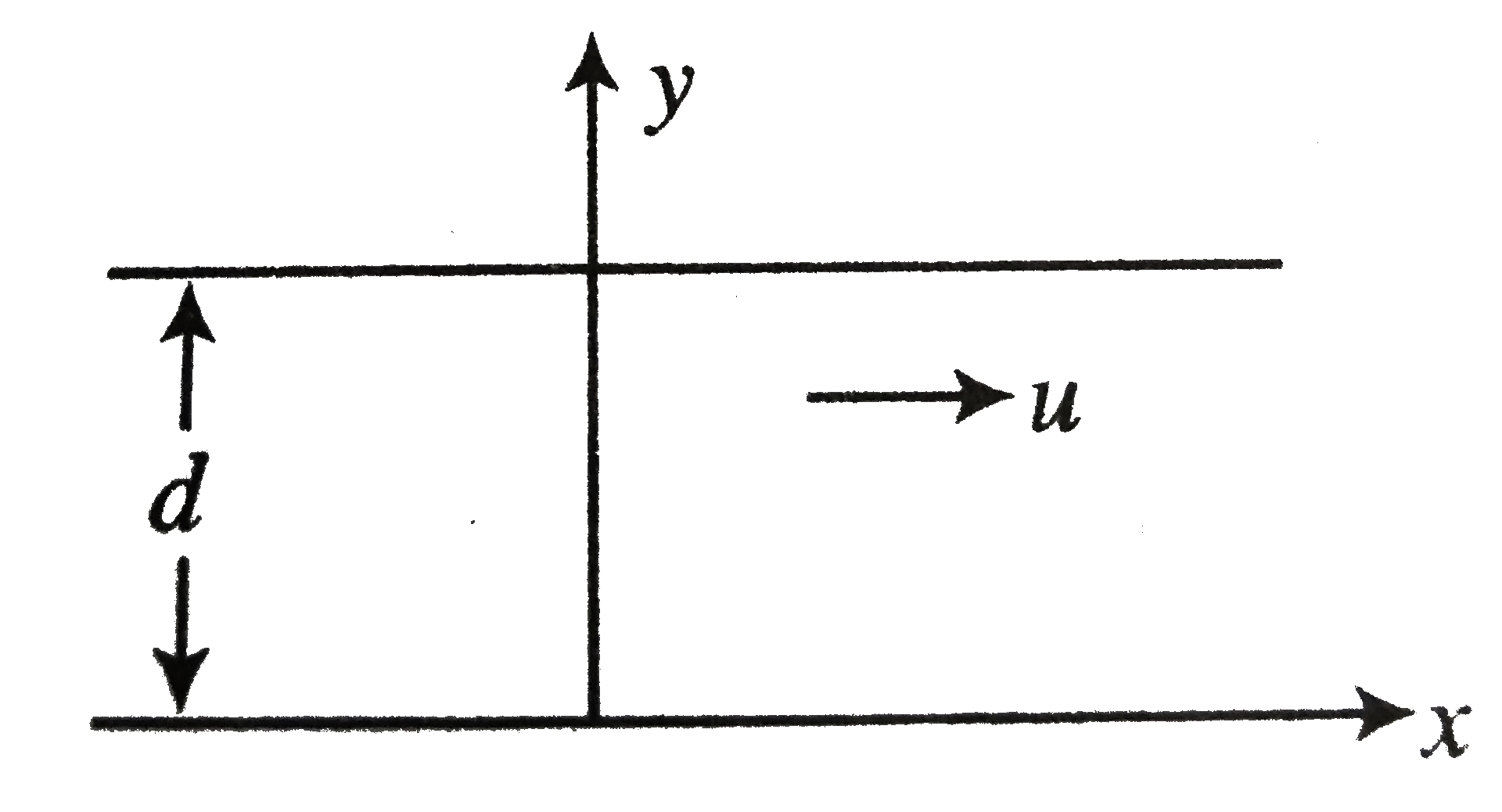
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.View Solution

