A cubical block of iron 5 cm on each side is floating on mercury in a vessel. (i) what is the height of the block above mercury level ?
(ii) Water is poured in the vessel until it just covers the iron block. What is the height of water column . density of mercury 13.6gm/cm3. Density of iron 7.2 gm/cm3
Case-I : Suppose h be the height of cubical block of iron above mercury.
Volume of iron block = 5 ×5 × 5 =125 cm3
Mass of iron block =125×7.2=900 gm
Volume of mercury displaced by the block
=5×5×(5–h) cm3
Mass of mercury displaced
=5×5(5–h)×13.6 gm
By the law floatation,
weight of mercury displaced = weight of iron block
5×5(5–h)×13.6=900
or (5−h)=90025×13.62.65
⇒ h=5−2.65=2.35 cm
Case - II :Suppose in this case height of iron block in water be x. The height of iron block in mercury will be (5 – x) cm.

Mass of the water displaced =5×5×(X)×1
Mass of mercury displaced =5×5×(5−x)×13.6
So, weight of water displaced +weight of mercury displaced=weight of iron block
or 5×5×x×1+5×5×(5−x)×13.6=900
or x=(5−x)×13.6=36
x=2.54cm
Topper's Solved these Questions
- FLUIDBOOK - MOTIONCHAPTER - FLUIDEXERCISE - Exercise
27 Videos
- FLUIDBOOK - MOTIONCHAPTER - FLUIDEXERCISE - Exercise-2 (level-I)
10 Videos
- ERRORS , THEORY BOOK - MOTIONCHAPTER - ERRORS , THEORY EXERCISE - EXERCISE 4 (LEVEL -II)
10 Videos
- GEOMETRICAL OPTICSBOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 4 | Level-II
55 Videos
Similar Questions
A cubical block of iron 5 cm on each side is floating on mercury in a vessel. (i) what is the height of the block above mercury level ?
(ii) Water is poured in the vessel unitl it just covers the iron block. What is the height of water column . density of mercur 13.6gm/cm3. Density of iron 7.2 gm/cm3
View Solution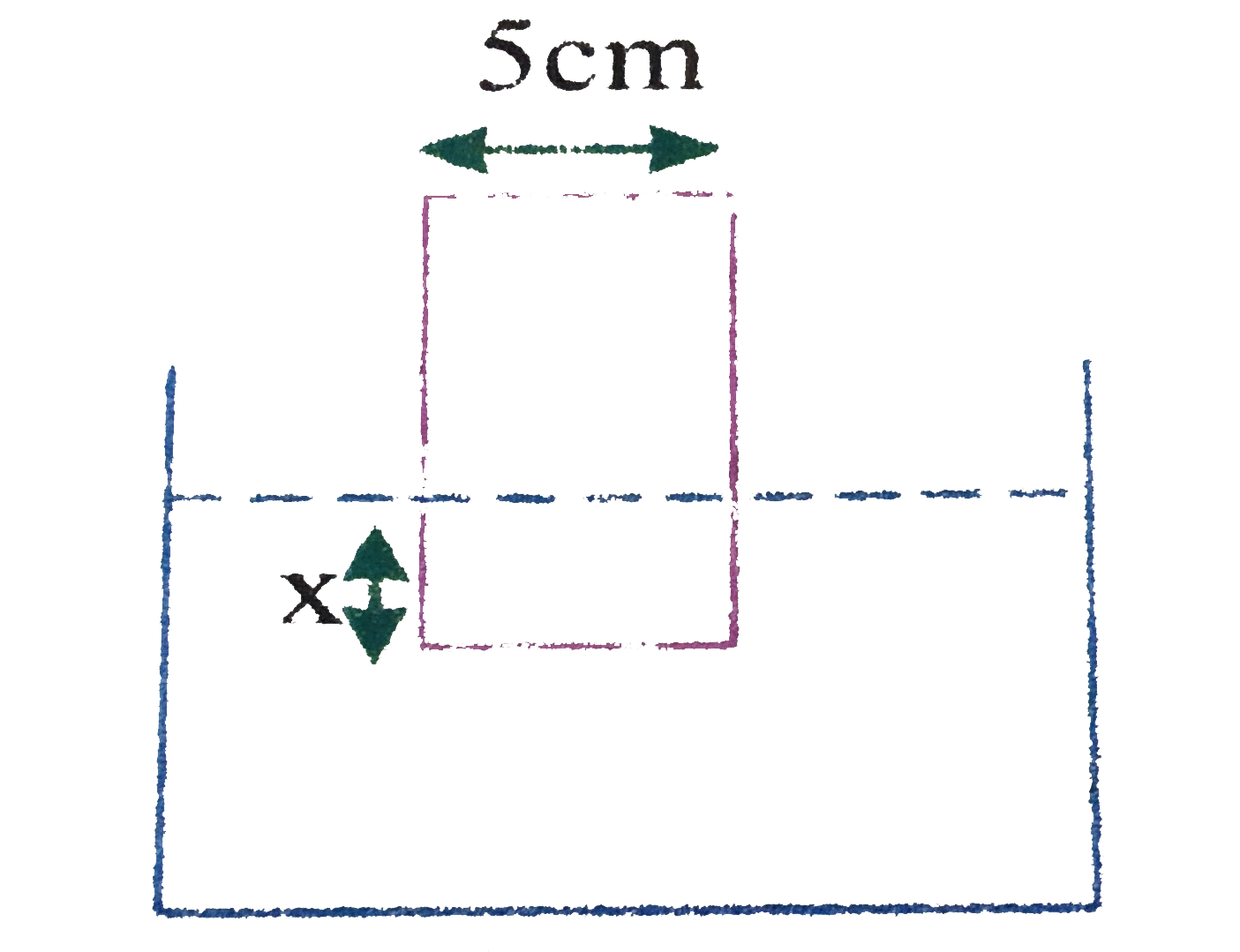
A cubical block of iron of side 5 cm is floating in mercury taken in a vessel. What is the height of the block above mercuery level.
(ρHg=13.6g/cm3,ρFe=7.2g/cm3)
View Solution
Knowledge Check
A cubical block of steel of each side equal to 1 is floating on mercury in vessel. The densities of steel and mercury are ρs and ρm. The height of the block above the mercury level is given by
Al(1+ρsρm)Bl(1−ρsρm)Cl(1+ρmρs)Dl(1−ρmρs)A cubical block of copper of side 10cm is floating in a vessel containing mercury. Water is poured into the vessel so that the copper block just gets submerged. The height of water column is
(ρHg=13.6g/cc,ρCu=7.3g/cc,ρwater=1gm/cc)A1.25 cmB2.5cmC5cmD7.5cm
What volume will 250 g of mercury occupy ? (Density of mercury =13.6 g cm−3)
View SolutionThe height of mercury which exerts the same pressure as 20 cm of water column, is
View SolutionAt a given place is barometer records a pressure of 70 cm of mercury. If the mercury in the barometer is replaced by water, what would be the height of the water column? Take density of mercury =13600kg/m3 density of water =1000kg/m3
View SolutionA cubical metal block of edge 12 cm floats in mercry with one fifth of the height inside the mercury. Water poured till the surface of the block is just immersed in it. Find the height of the block is just immersed in it. Find the height of the water column to be poured. Specific gravity of mercury =13.6.
View SolutionIf the mercury in the barometer is replaced by water what will be the resulting height of the water column?
Density of water =1000kgm−3 density of mercury =13600kgm−3
View SolutionIf the mercury in the barometer is replaced by water, what will be the resulting height of the water column? Density of water =1000kgm−3 density of mercury =13600kgm−3
View Solution
