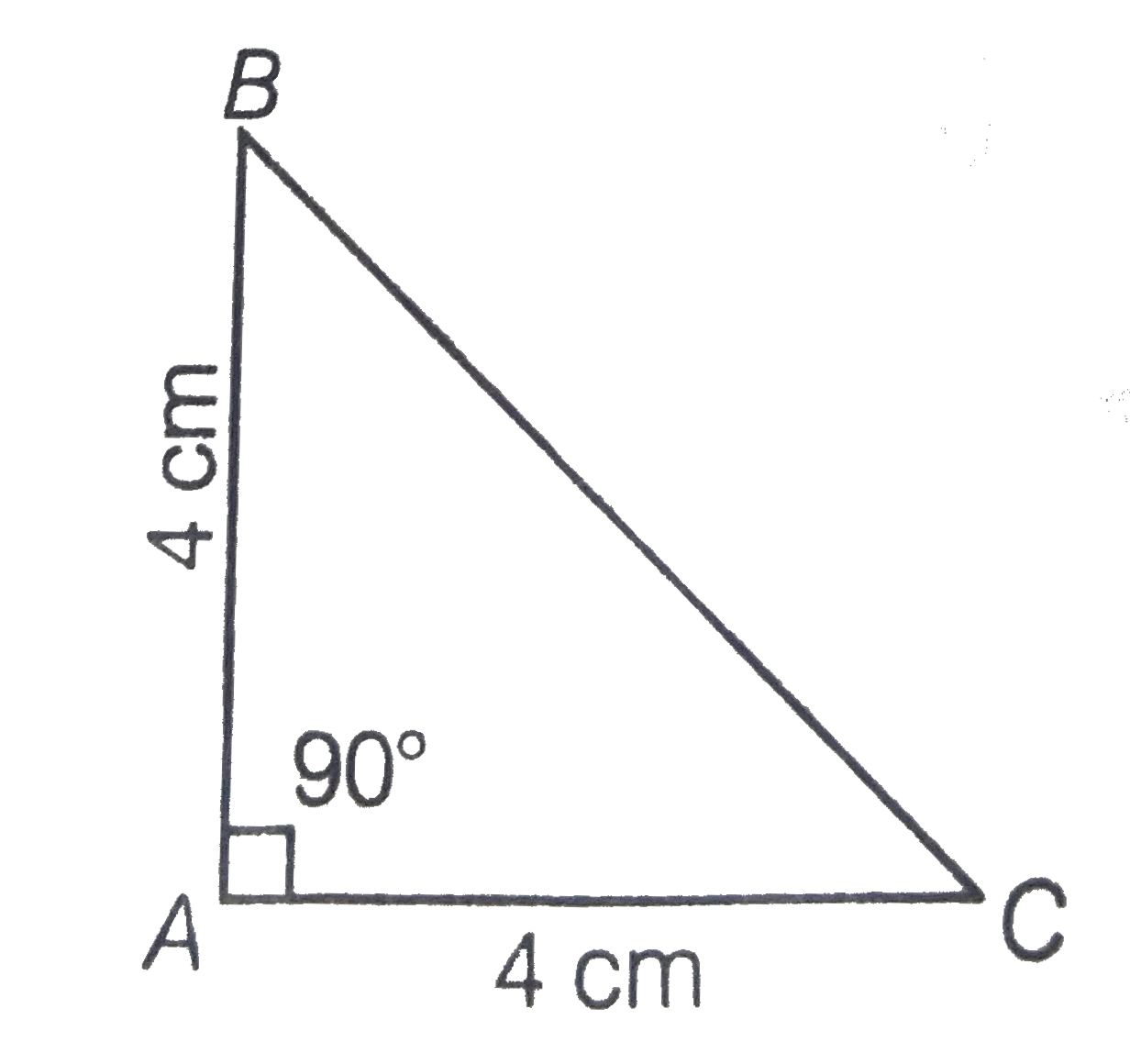
The area of $△ A B C$ is $8 c m^{2}$ in which $A B = A C = 4 c m$ and $∠ A = 90^{\circ}$ .

A

true

B

false

C

can not detemine

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

We have, $A B C$ is a right angled triangle at $A$ , where sides are given $A B = A C = 4 c m$
$∴ Area of a triangle A B C = \frac{1}{2} (Base \times Height) = \frac{1}{2} \times A C \times A B = \frac{1}{2} \times 4 \times 4 = 8 c m^{2}$

|

Updated on:21/07/2023

Class 9 MATHS HERONS FORMULA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the area of a parallelogram ABCD in which AB = 8 cm, BC = 15 cm and diagonal AC = 17 cm.
A $220 c m^{2}$
B $150 c m^{2}$
C $120 c m^{2}$
D $175 c m^{2}$
Question 2 - Select One
The area of $△ A B C$ is $88 c m^{2}$ . If D is the midpoint of BC and E is the midpoint of AB, then the area (in $c m^{2}$ ) of $△ B D E$ is:
A44
B22
C11
D5.5
Question 3 - Select One
Let ABC be a triangle with $∠ B = 90^{\circ}$ . Let AD be the bisector of $∠ A$ with D on BC. Supose AC = 6 cm and the area of the triangle ADC is 10 $c m^{2}$ . Then the length of BD in cm is equal to
A $\frac{3}{5}$
B $\frac{3}{10}$
C $\frac{5}{3}$
D $\frac{10}{3}$

NCERT EXEMPLAR-HERON'S FORMULA-Herons Formula

Home
Ask Doubt
Profile