Two chords AB and AC of a circle subtends angles equal to $90^{\circ} and 150^{\circ}$ , respectively at the centre. Find $∠ B A C$ , if AB and AC lie on the opposite sides of the centre.

Video Solution

Text Solution

Verified by Experts

In $Δ B O A, O B = O A$ [both are the radius of circle]
$∴ ∠ O A B = ∠ O B A \dots (i)$
[angles opposite to equal sides are equal]

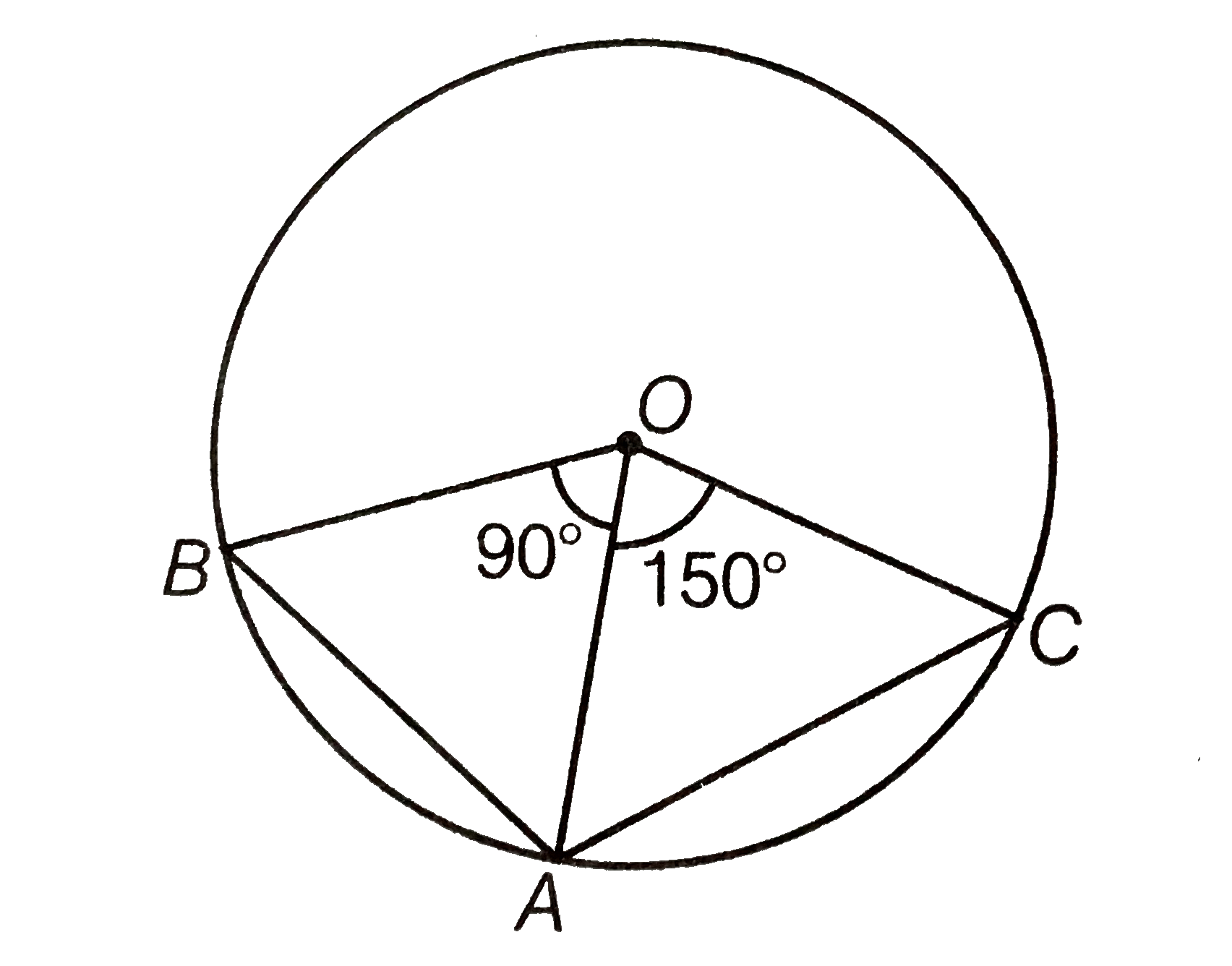
In $Δ O A B, ∠ O B A + ∠ O A B + ∠ A O B = 180^{\circ}$ [by angle sum property of a triangle]
$\Rightarrow ∠ O A B + ∠ O A B + 90^{\circ} = 180^{\circ}$ [from Eq. (i)]
$\Rightarrow 2 ∠ O A B = 180^{\circ} - 90^{\circ}$
$\Rightarrow ∠ O A B = \frac{90^{\circ}}{2} = 45^{\circ}$
Now, in $Δ A O C, A O = O C$ [both are the redius of a circle]
$∴ ∠ O C A = ∠ O A C$ ...(ii)
[angles opposite to equal sides are equal]
Also, $∠ A O C + ∠ O A C + ∠ O C A = 180^{\circ}$ [by angle sum property of a triangle]
$\Rightarrow 150^{\circ} + 2 ∠ O A C = 180^{\circ}$ [from Eq. (ii)]
$\Rightarrow 2 ∠ O A C = 180^{\circ} - 150^{\circ}$
$\Rightarrow 2 ∠ O A C = 30^{\circ}$
$\Rightarrow ∠ O A C = 15^{\circ}$
$∴ ∠ B A C = ∠ O A B + ∠ O A C = 45^{\circ} + 15^{\circ} = 60^{\circ}$

|

Updated on:21/07/2023

Class 9 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR-CIRCLES-Exercise 10.4

Home
Ask Doubt
Profile