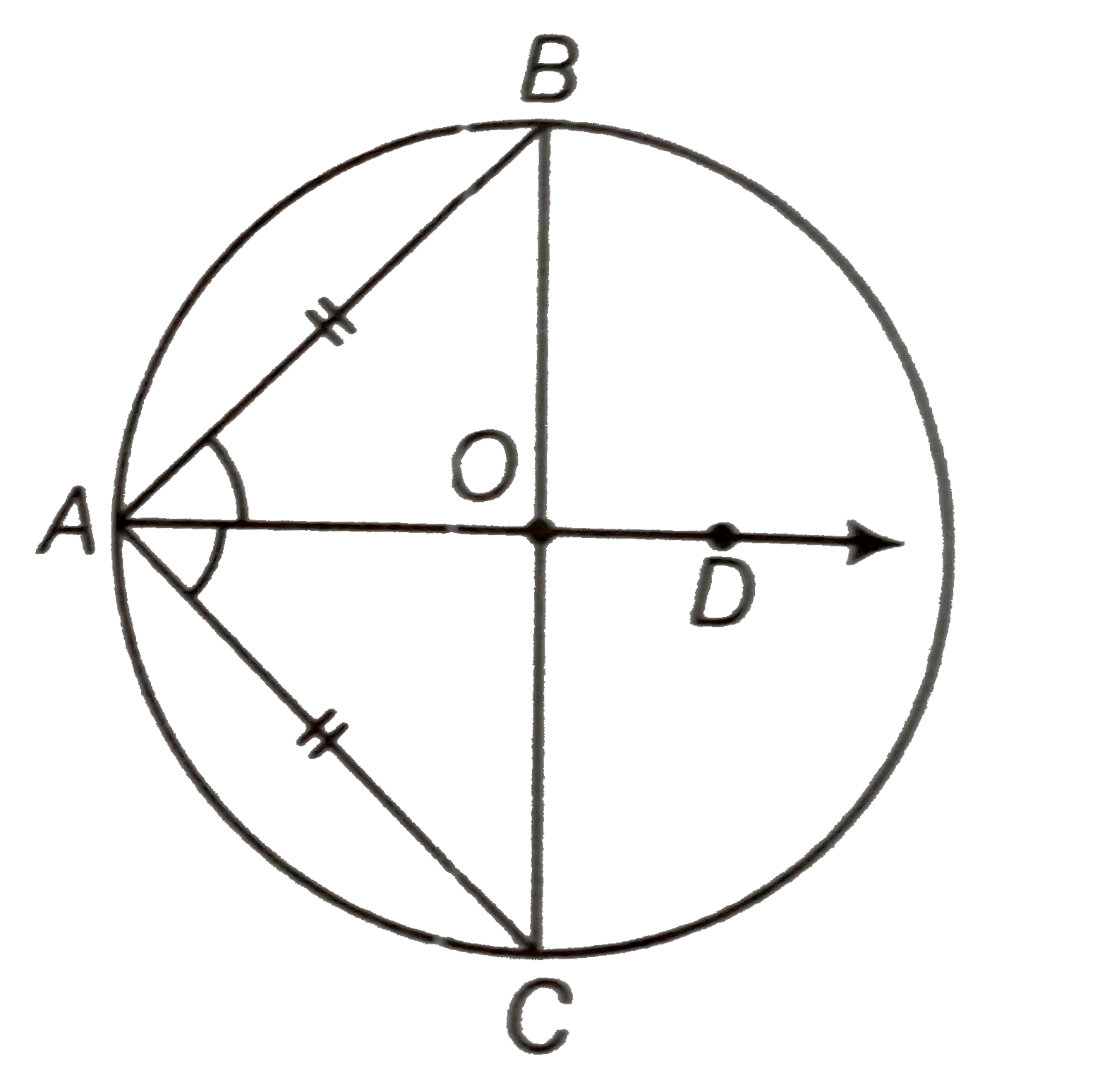
Two chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the angle bisector of ∠BAC.
Given AB and AC are two equal chords whose centre is O.
To prove Centre O lies on the bisector of ∠BAC.
Construction Join BC, draw bisector AD of ∠BAC.
Proof In ΔBAMandΔCAM,
AB=AC [given]
∠BAM=∠CAM [given]
and AM=AM [common side]
∴ΔBAM≅ΔCAM [by SAS congruence rule]
⇒BM=CM [by CPCT]
and ∠BMA=∠CMA [by CPCT]
So, BM=CMand∠BMA=∠CMA=90∘
So, AM is the perpendicular bisector of the chord BC.
Hence, bisector of ∠BAC i.e., AM passes through the centre O.
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Knowledge Check
If the length of a chord of a circle is equal to that of the radius of the circle , then the angle subtended , in radians , at the centre of the circle by the chord is
A1Bπ2Cπ3Dπ4
If two chords AB and AC of a circle with centre O are such that the centre O lies on the bisector of ∠BAC; Prove that AB=AC
View SolutionIf two chords AB and AC of a circle with centre O are such that the centre O lies on the bisector of ∠BAC, prove that AB=AC , i.e. the chords are equal.
View SolutionEqual chords of a circle are equidistant from the centre.
View SolutionEqual chords of a circle subtend equal angles at the centre.
View SolutionProve that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
View SolutionState and prove that :
Theorem 10.1 : Equal chords of a circle subtend equal angles at the centre
View SolutionTheorem:-4(iii) If two equal chords are drawn from a point on the circle; then the centre of a circle will lie on angle bisector of these two chords .
View Solution
