AD is a diameter of a circle and AB is a chord. If AD = 34cm, AB = 30cm, the distance of AB form the centre of the circle is
17 cm
15 cm
4 cm
8 cm
The correct Answer is:D
Given, AD = 34 cm and AB = 30 cm
In figure, draw OL⊥AB.
Since, the perpendicular from the centre of a circle to a chord bisects the chord.
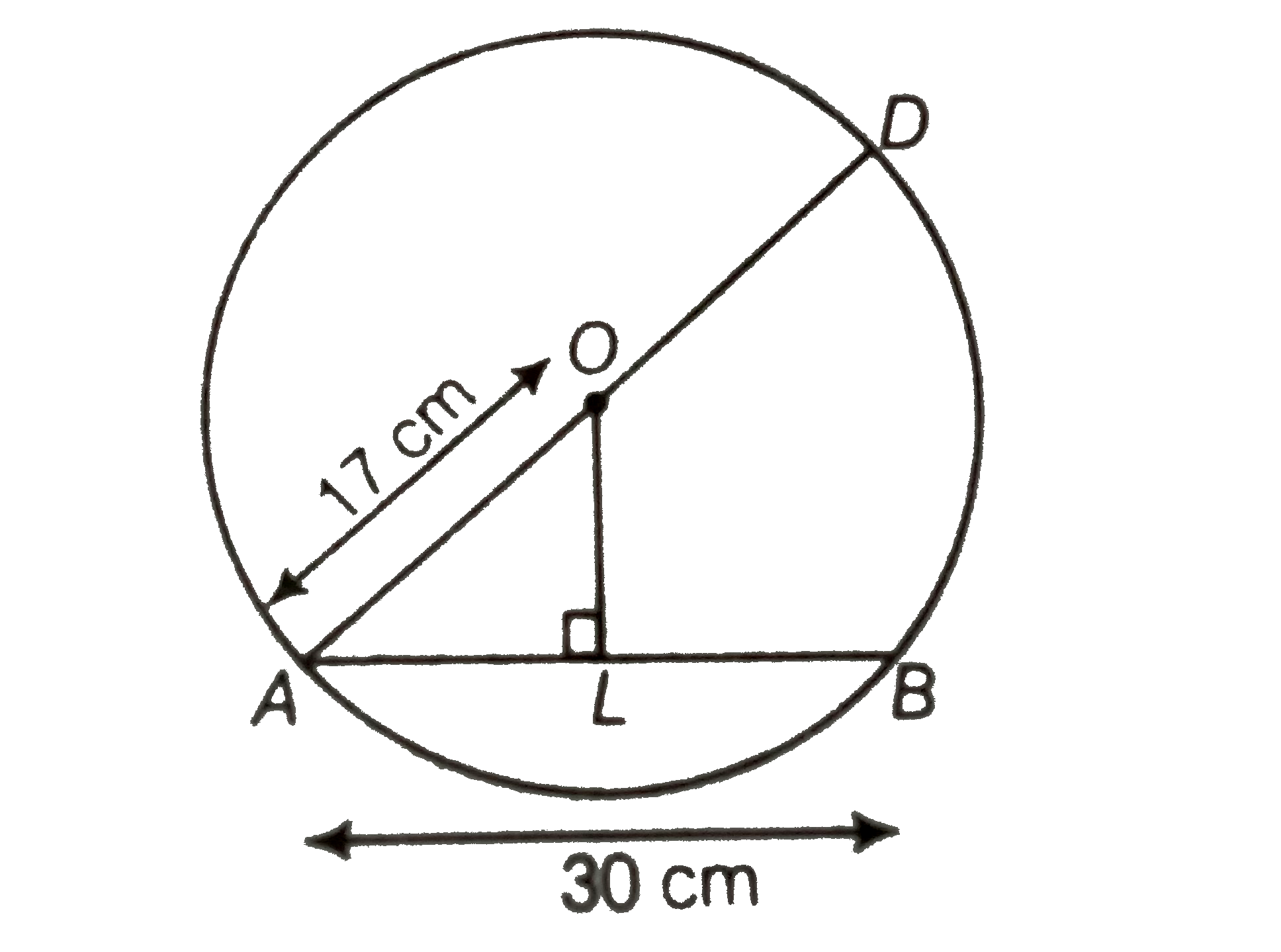
∴AL=LB=12AB=15cm
In right angled ΔOLA,OA2=OL2+AL2[by pythagoras theorem]
∴(17)2=OL2+(15)2
⇒289=OL2+225
⇒OL2=289−225=64
∴OL=8cm
[taking positive square root, because length is always positive]
Hence, the distance of the chord from the centre is 8 cm.
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
AD is the diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is
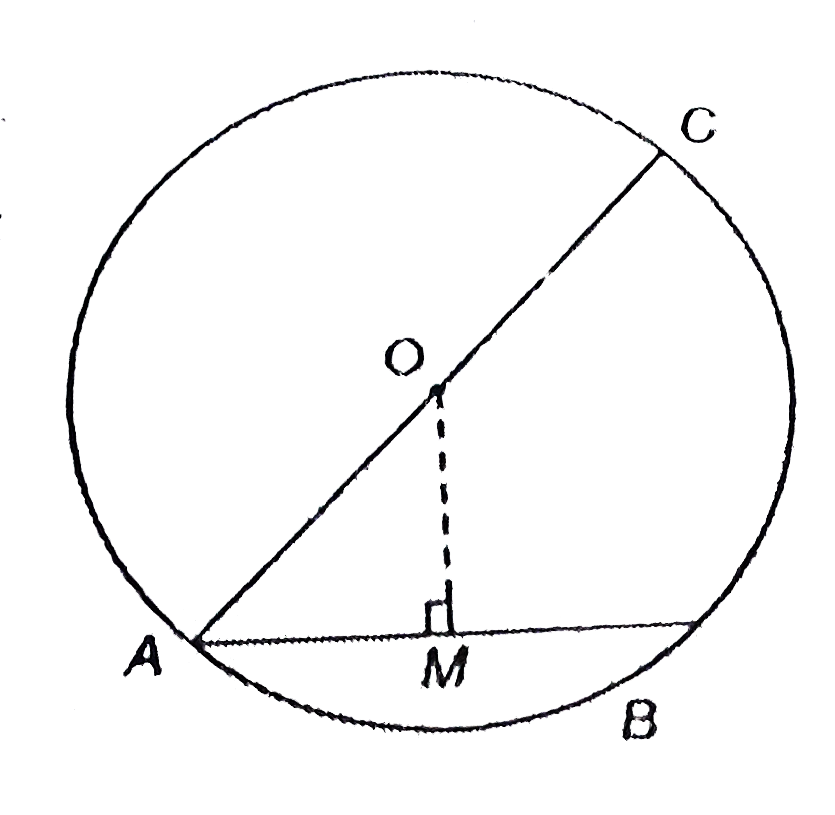
View SolutionIn the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.
View Solution
Knowledge Check
In the adjoining figure, O is the centre of circle and diameter AC=26cm. If chord AB=10cm, then the distance between chord AB and centre O of the circle is :
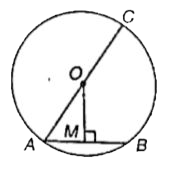 A24 cmB16 cmC12 cmDnone of the above
A24 cmB16 cmC12 cmDnone of the aboveIn a class of 39 students the ratio of boys and girls is 2 : 1. Radhika ranks 15th among all the students from top and 8th among girls from bottom. How many boys are there below Radhika ?
AA) 9BB) 17CC) 11DD) 15O' is the centre of the circle, AB is a chord of the circle, OM⊥AB. If AB=20cm,OM=2√11 cm, then radius of the circle is
A15 cmB12 cmC10 cmD11 cm
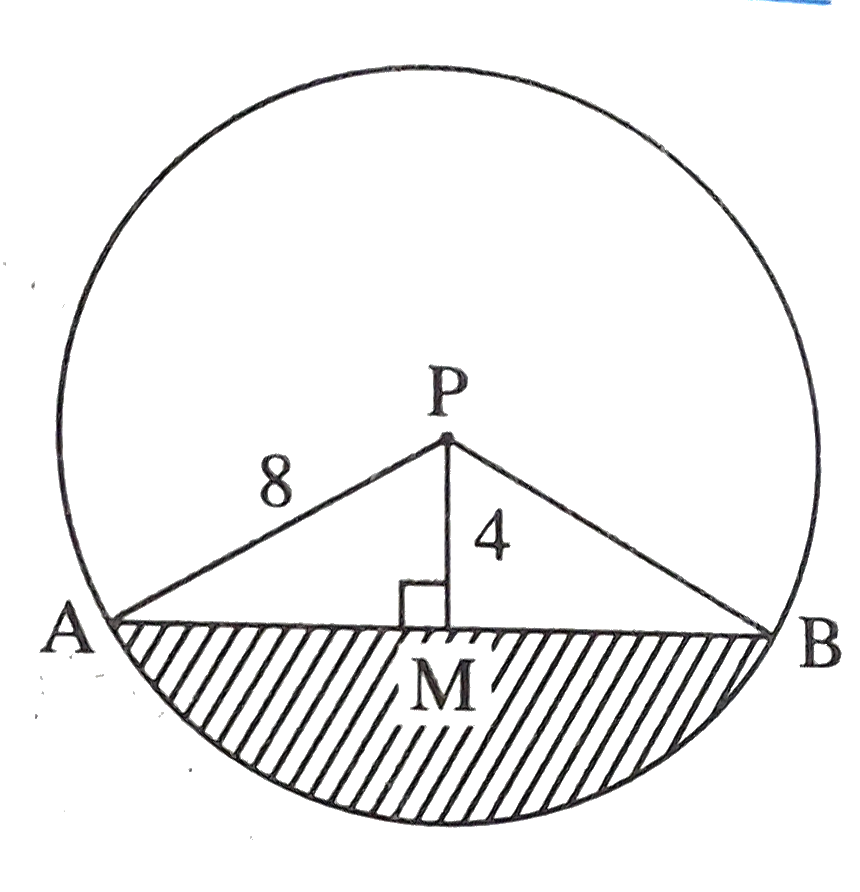
In the figure, seg AB is a chord of a circle with centre P. If PA = 8 cm and distance of chord AB from the centre P is 4 cm, find the area of the shaded portion.
View SolutionAB is a chord of a circle with centre O and diameter 20 cm. If AB = 12 cm, find the distance of AB from O.
View SolutionAB and CD are parallel chords of a circle 3 cm apart. If AB = 4 cm, CD = 10 cm, then what is the radius of the circle ?
View SolutionRadius of a circle is 34 cm and the distance of the chord from the centre is 30 cm, find the length of the chord .
View SolutionA circle is drawn on AB as diameter. The centre of the circle is O and the length AB = 13 cm. P is a point on the circumference of the cirlces such that the chord AP = 12 cm. Calculate the value of the angles PAB and POB in radians :
View Solution
