Question

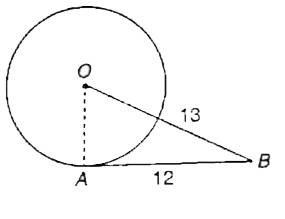
A circle is drawn on AB as diameter. The centre of the circle is O and the length AB = 13 cm. P is a point on the circumference of the cirlces such that the chord AP = 12 cm. Calculate the value of the angles PAB and POB in radians :

Options

A. `0.395, 0.789`
B. `0.786, 0.735`
C. `0.389.0.689`
D. `0.786,0.753`

Answer

A

Explanation

To solve the problem step by step, we will follow these instructions:

Step 1: Identify the given information
- The diameter \( AB = 13 \, \text{cm} \)
- The length of the chord \( AP = 12 \, \text{cm} \)
- The center of the circle \( O \)

Step 2: Calculate the radius of the circle
Since \( AB \) is the diameter, we can find the radius \( r \) of the circle:
\( r = \frac{AB}{2} = \frac{13}{2} = 6.5 \, \text{cm} \)

Step 3: Use the Pythagorean theorem in triangle \( APB \)
In triangle \( APB \), we can apply the Pythagorean theorem since \( \angle APB \) is a right angle (angle in a semicircle):
\( AB^2 = AP^2 + PB^2 \)
Substituting the known lengths:
\( 13^2 = 12^2 + PB^2 \)
Calculating the squares:
\( 169 = 144 + PB^2 \)
Rearranging gives:
\( PB^2 = 169 - 144 = 25 \)
Taking the square root:
\( PB = \sqrt{25} = 5 \, \text{cm} \)

Step 4: Calculate angle \( PAB \)
Now we can find angle \( PAB \) using the tangent function:
\( \tan(PAB) = \frac{PB}{AP} = \frac{5}{12} \)
To find \( PAB \):
\( PAB = \tan^{-1}\left(\frac{5}{12}\right) \)
Calculating this gives:
\( PAB \approx 0.395 \, \text{radians} \)

Step 5: Calculate angle \( POB \)
Since \( O \) is the center of the circle, angle \( POB \) is twice angle \( PAB \):
\( POB = 2 \times PAB = 2 \times 0.395 \approx 0.790 \, \text{radians} \)

Summary of Results
- \( PAB \approx 0.395 \, \text{radians} \)
- \( POB \approx 0.790 \, \text{radians} \)