Diagonals AC and BD of a parallelogram ABCD intersect each other at O. If OA= 3 cm and OD = 2 cm, determine the lengths of AC and BD.
Video Solution
Text Solution
Given, ABCD is a parallelogram OA = 3 cm and OD = 2 cm
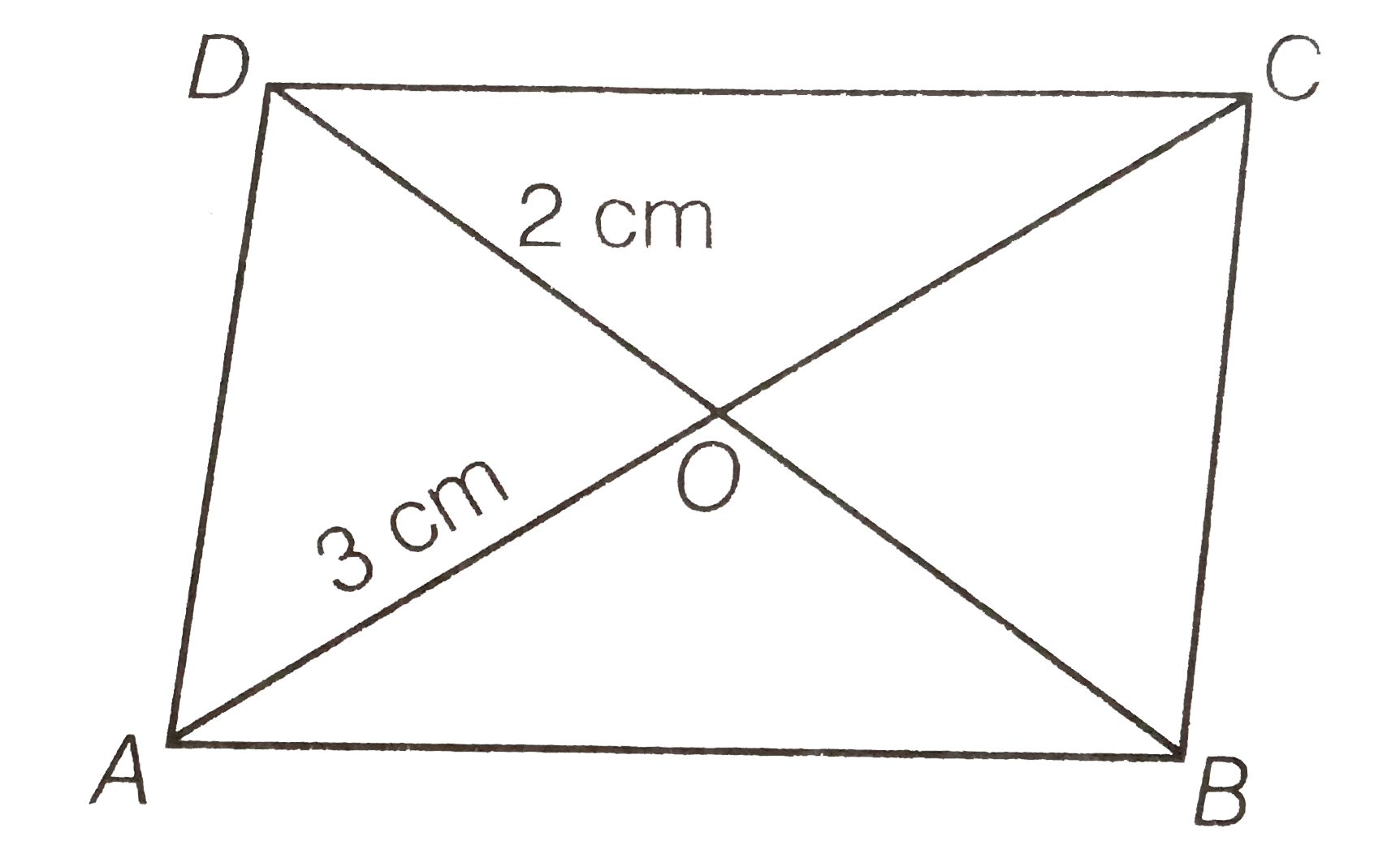
We know that, diagonals of a parallelogram bisect each other.
∴ Diagonal AC = 2 OA = 6 cm [∵ AO = OC]
and Diagonal BD = 2 OD = 4 cm [∵ BO= OD]
Hence, the length of the diagonals AC and BD are 6 cm and 4 cm, respectively.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Diagonals AC and BD of a parallelogram ABCD intersect at O. If OA = 3 cm and OD = 2 cm, determine the lengths of AC and BD.
AAC=6cm,BD=2cmBAC=6cm,BD=4cmCAC=3cm,BD=4cmDAC=3cm,BD=3cmThe diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, then ∠DBC is equal to
A24∘B86∘C38∘D32∘The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, then ∠DBC is equal to
A24∘B86∘C38∘D32∘
If ACandBD are diagonals of a parellelogram ABCD, show that
View SolutionThe diagonals AC and BD of a quadrilateral ABCD intersect at point 'O'. If BO = OD, then prove that the areas of ΔABCandΔADC are equal
View SolutionDiagonals ACandBD of a trapezium ABCD with AB∣∣DC intersect each other at O . Prove that ar(AOD)=ar(BOC) .
View SolutionIn rhombus ABCD, diagonals AC and BD intersect each other at point O If cosine of angle CAB is 0.6 and OB 8 cm, find the lengths of the side and the diagonals of the rhombus.
View SolutionThe diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, find ∠DBC.
View Solution
