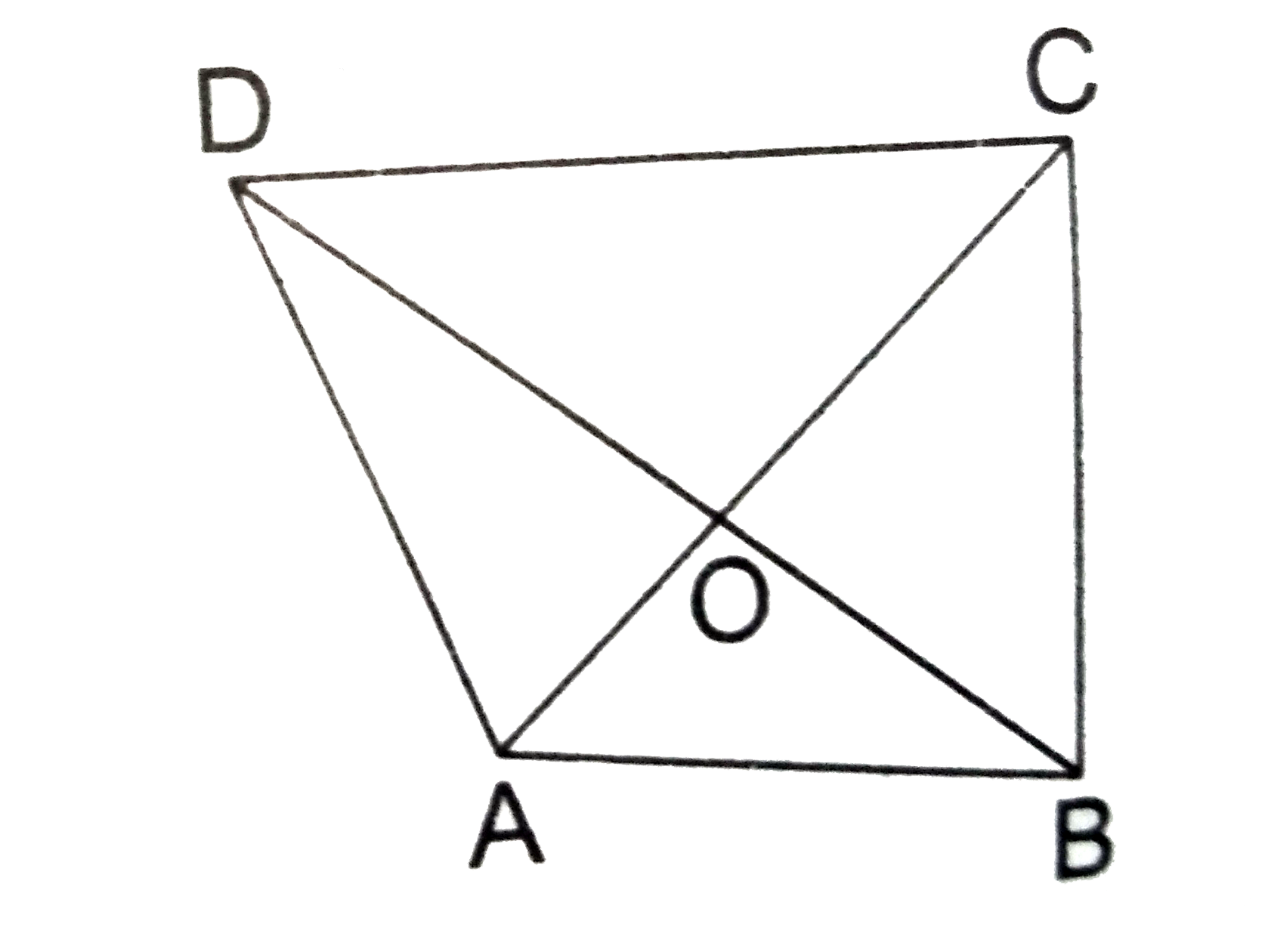
The diagonals AC and BD of a quadrilateral ABCD intersect at point 'O'. If BO = OD, then prove that the areas of ΔABCandΔADC are equal
In □ABCD, the diagonals AC and BD intersect at 'O' such that
BO=OD
Now, in ∠ABD,O is the mid-point of BD
∴ are of ΔABO= area of ΔADO
(∴ median divides the triangle into two equal areas)...(1)
In ΔCBD,O is the mid-point of BD
∴ area of ΔCBO= area of ΔCDO
(∴ medians divides the triangle into two equal area)...(2)

Adding (1) and (2)
area of ΔABO+ area of ΔCBO= area of ΔADO+ area of ΔCDO
⇒ area of ΔABC= area of ΔADC
Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Problems From NCERT/exemplar
12 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise
34 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )
5 Videos
Similar Questions
In the figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that

ar(ΔDOC) = ar(ΔAOB)
View SolutionIn the figur e, diagonals AC and BD of quadrilateral A BCD intersect at 0 such that OB = OD. If AB = CD, then show that

ar(ΔDCB) = ar(ΔACB)
View Solution
Knowledge Check
Diagonals AC and BD of a quadrilateral intersect at O. It AO:OC=1:2=BO:ODandAB=16cm then DC is
A16cmB8cmC4cmD32cmDiagonals AC and BD of a parallelogram ABCD intersect at O. If OA = 3 cm and OD = 2 cm, determine the lengths of AC and BD.
AAC=6cm,BD=2cmBAC=6cm,BD=4cmCAC=3cm,BD=4cmDAC=3cm,BD=3cmThe diagonals AC and BD of a cyclic quadrilateral ABCD intersect each other at the point P. Then,it is always true that
AAP. CP = BP. DPBAP.BP = CP. DPCAP. CD = AB. CPDBP. AB = CD.CP
In Fig 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD.If AB=CD , then show that
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
View SolutionIn the figure, diagonals AC and BD of quadrilateral ABCD intersect at 0 such that OB = OD. If AB = CD, then show that

DA I I CB or ABCD is a parallelogram.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(ΔAOD) = ar(ΔBOC). Prove that ABCD is a trapezium.
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect point O. Prove that :
AB+BC+CD+DA<2(AC+BD)

View Solution
