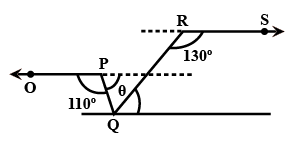
In the given figure, if OP||Rs,∠OPQ=110∘and∠QRS=130∘,then∠PQR is equal to
A
40∘
B
50∘
C
60∘
D
70∘
Video Solution
Text Solution
The correct Answer is:C
In the given figure producing OP, to intersect RQ at X.
Since, OP||RS and RX is a transversal.
So, ∠RXP=∠XRS [alternate angles]
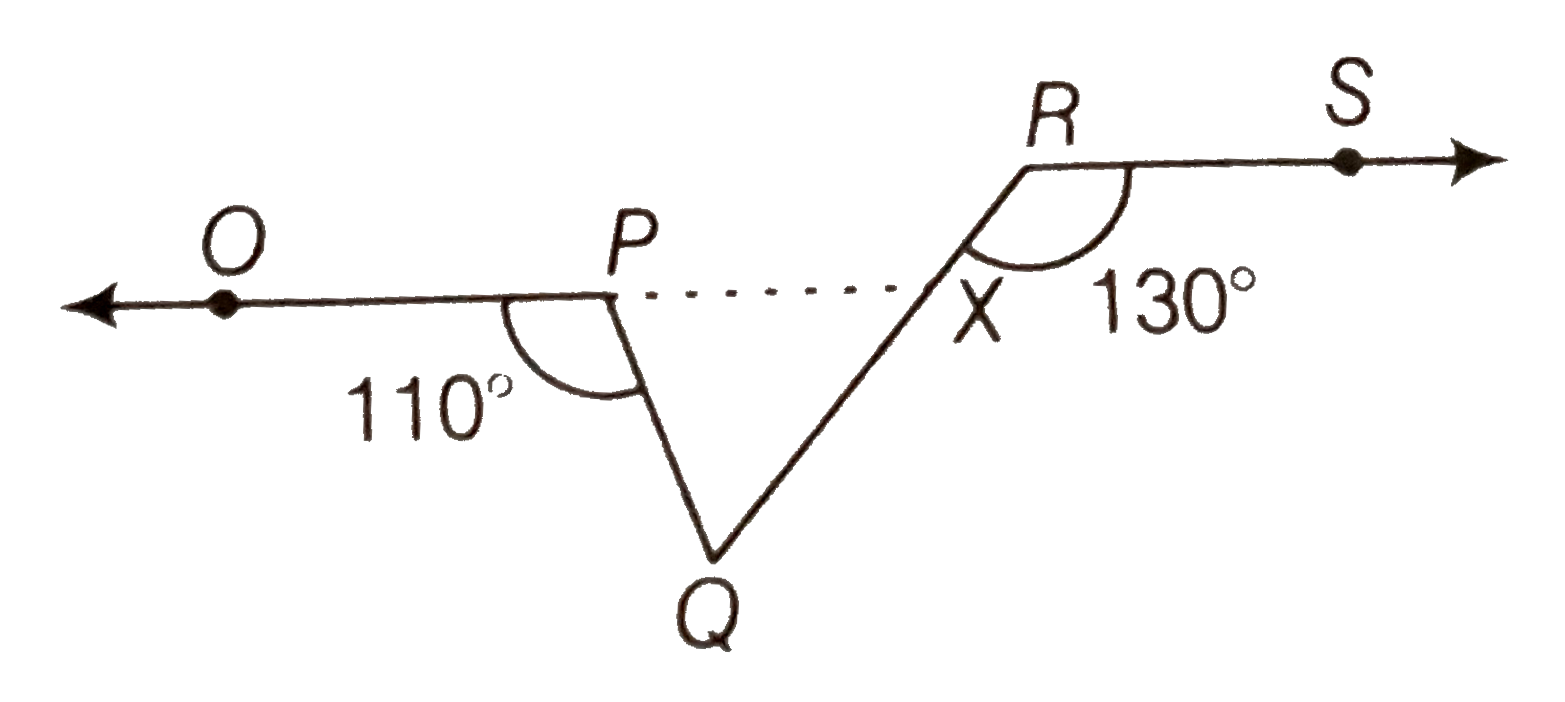
⇒ ∠RXP=130∘ [∴∠QRS=130∘(given)]..(i)
Now, RQ is a line segment.
So, ∠PXQ+∠RXP=180∘ [linear pair axiom]
⇒ ∠PXQ=180∘−∠RXP=180∘−130∘ [from Eq. (i)]
⇒ ∠PXQ=50∘
InΔPQX,∠OPQ is an exterior angle , " "
∴ ∠OPQ=∠PXQ+∠PQX [∴exterior angle = sum of two opposite interior angles ]
⇒ 110∘=50∘+∠PQX
⇒ ∠PQX=110∘−50∘
∴ ∠PQR=60∘ [∴∠PQX=∠PQR]
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In figure, if AB || CD || EF, PQ || RS, ∠ RQD =25∘ and ∠ CQP =60∘, then ∠QRS is equal to
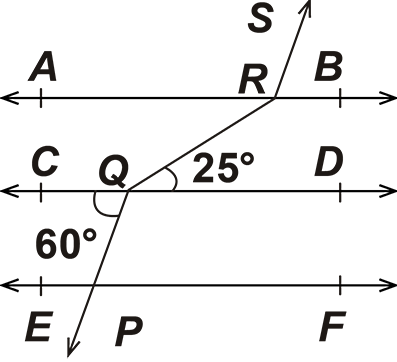 A85∘B135∘C145∘D110∘
A85∘B135∘C145∘D110∘In the given figure, AB11 CD. If ∠ABO=130∘ and ∠OCD=110∘, then ∠BOC is equal to
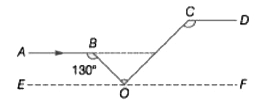 A50∘B60∘C70∘D90∘
A50∘B60∘C70∘D90∘In the given figure, if OP bisects ∠BOC and OQ bisects ∠AOC, then ∠POQ is equal to
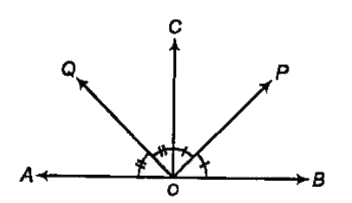 A90∘B75∘C105∘D80∘
A90∘B75∘C105∘D80∘
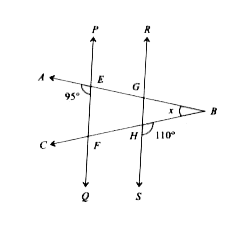
In the given figure PQ is parallel to RS, ∠AEF=95∘,∠BHS=110∘, and ∠ABC=x∘ . Then what is the value of x ?
View SolutionIn fig. 6.31, if PQ is parallel to ST ∠PQR = 110 and ∠RST=130 find ∠QRS
View SolutionIn the given figure, ∠OAB=110∘ and ∠BCD=130∘ then ∠ABC is equal to
View SolutionIn the given figure, AB|| CD. If ∠AOC=40∘and∠OAB=110∘ then ∠OCD equals
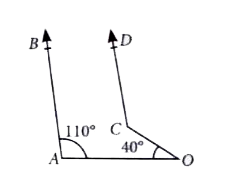
View SolutionIf P,Q,R are three points which lie on the circle with centre O such that ∠POQ=110∘,∠QOR=130∘, then ∠PQR=……..
View Solution


