The random variable X has a probability distribution P(X) of the following form, where k is some number : P(X) = {(k,ifx=0),(2k,ifx=1),(3k,ifx=2),(otherwise) (a) Determine k. (b) Find P (X<2) , P (X≤2) , P(X≥2)
AS Sum of all probabilities should be 1
=k+2k+3k=1→k=16
(ii) P(X<2)=P(X=0)+P(X=1)
=k+2k
=3{k}
=36
=12
P(X≤2)=P(X=0)+P(X=1)+P(X=2)
=k+2k+3k
=6{k}
=6×16
=66
=1
P(X≥2)=P(X=2)+P(X>2)
=3k+0
=3×16
=36
=12
Topper's Solved these Questions
Similar Questions
The random variable X has a probability distribution P(X) of the following form, where k is some number :P(X) = {(k,ifx=0),(2k,ifx=1),(3k,ifx=2),(0otherwise)(a) Determine k.(b) Find P (X<2) , P (X≤2) , P(X≥2)
View SolutionThe random variable 'X' has a probability distribution P (X) of the following form, where k is some number :
P(X)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩k,ifX=02k,ifX=13k,ifX=20,ifotherwise
(a) Determine the value of k.
(b) Find P(X<2),P(X≤2),P(X≥2)
View Solution
Knowledge Check
If X is the a random variable with probability mass function P(x)=kx, for x = 1,2,3
= 0 , otherwise
then k = ……..A15B14C16D23
A random variable 'X' has a probability distribution P(X) of the following form (k is constant):

then k = __________ .
View SolutionThe probability distribution of X is as follows:
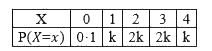
Find k and P [X<2].
View SolutionA random variable X has the following probability distribution:
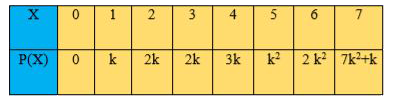
Determine : (i) k (ii) P(X<3) (iii) P(X>4)
View SolutionA random variable 'X' has the following probability distribution :

Find : (i) the value of K (ii) P(X≤1)
(iii) P(X≥0).
View SolutionA random variable X has the following probability distribution:Determine (i) k (ii) P(X<3)(iii) P(X>6) (iv) P(0<X<3)
View SolutionIf a random variable X has a poisson distribution such that P(X=1)=P(X=2), its mean and variance are
View SolutionA random variable X has the following probability distribution: X=xi: 1 2 3 4 P(X=xi): k 2k 3k 4k Write the value of P(X≥3) .
View Solution
