The random variable X has a probability distribution P(X) of the following form, where k is some number :P(X) = {(k,ifx=0),(2k,ifx=1),(3k,ifx=2),(0otherwise)(a) Determine k.(b) Find P (X<2) , P (X≤2) , P(X≥2)
(i)As, we know,
Sum of all probablities in a probablity distribution is 1.
So, in this question,
k+2k+3k+0=1⇒6k=1
⇒k=16 which is the required value.
(ii)(a)P(X<2)=P(X=0)+P(X=1)
=k+2k=3k=3(16)=12
(b)P(X≤2)=P(X=0)+P(X=1)+P(X=2)
=k+2k+3k=6k=6(16)=1
(b)P(X≥2)=P(X=2)+0
=3k=12
Topper's Solved these Questions
- PROBABILITYBOOK - NCERTCHAPTER - PROBABILITYEXERCISE - Solved Examples
36 Videos
- PROBABILITYBOOK - NCERTCHAPTER - PROBABILITYEXERCISE - EXERCISE 13.1
17 Videos
- PROBABILITYBOOK - NCERTCHAPTER - PROBABILITYEXERCISE - EXERCISE 13.2
18 Videos
- MATRICESBOOK - NCERTCHAPTER - MATRICESEXERCISE - EXERCISE 3.3
12 Videos
- RELATIONS AND FUNCTIONSBOOK - NCERTCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 1.3
14 Videos
Similar Questions
The random variable 'X' has a probability distribution P (X) of the following form, where k is some number :
P(X)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩k,ifX=02k,ifX=13k,ifX=20,ifotherwise
(a) Determine the value of k.
(b) Find P(X<2),P(X≤2),P(X≥2)
View SolutionA random variable 'X' has a probability distribution P(X) of the following form (k is constant):

then k = __________ .
View Solution
Knowledge Check
If X is the a random variable with probability mass function P(x)=kx, for x = 1,2,3
= 0 , otherwise
then k = ……..A15B14C16D23
The probability distribution of X is as follows:
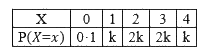
Find k and P [X<2].
View SolutionA random variable 'X' has the following probability distribution :

Find : (i) the value of K (ii) P(X≤1)
(iii) P(X≥0).
View SolutionA random variable X has the following probability distribution:
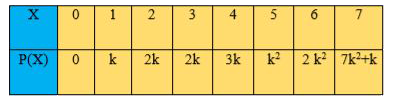
Determine : (i) k (ii) P(X<3) (iii) P(X>4)
View SolutionA random variable X has the following probability distribution:Determine (i) k (ii) P(X<3)(iii) P(X>6) (iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution: X=xi: 1 2 3 4 P(X=xi): k 2k 3k 4k Write the value of P(X≥3) .
View SolutionLet X denote the number of hours you study during a randomly selected school day. The probability that X take the values of x has the following form, where k is some unknown constant. P(X=x)={(0.1ifx=0),(kx,ifx=1or2),(k(5−x),ifx=3or4),(0,otherwise)
Find:
(i) k
(ii) the probability that you study exactly two hours,
(iii) the probability that you study at most two hours.
View SolutionA random variable X has the following probability distribution :

Determine
(i) k (ii) P(X<3)
(iii) P(X>6) (iv) P(0<X<3).
View Solution
