Solve the following system of linear inequalities
3x+2y≥24,3x+y≤15,x≥4.
Video Solution
Text Solution
Consider the inequation 3x+2y≥24 as an equation, we have 3x+2y=24.
⇒2y=24−3x
x084y1206
Hence, line 3x+y=24 intersect coordinate axes at points (8, 0) and (0, 12).
Now, (0, 0) does not satisfy the inequation 3x+2y≥24.
Therefore, half plane of the solution set does not contains (0, 0).
Consider the inequation 3x+y≤15 as an equation, we have
3x+y=15
⇒y=15−3x
x053y1506
Line 3x+y=15 intersects coordinate axes at points (5, 0) and (0, 15) .
Now, point (0, 0) satisfy the inequation 3x+y≤15 .
Therefore, the half plane of the solution contain origin.
Consider the inequality x≤4 as an equation, we have
x = 4
It represents a straight line parallel to Y-axis passing through (4, 0) . Now, point (0, 0) does not satisfy the inequation x≥4.
Therefore, half plane does not contains (0, 0),
The graph of the above inequations is given below.
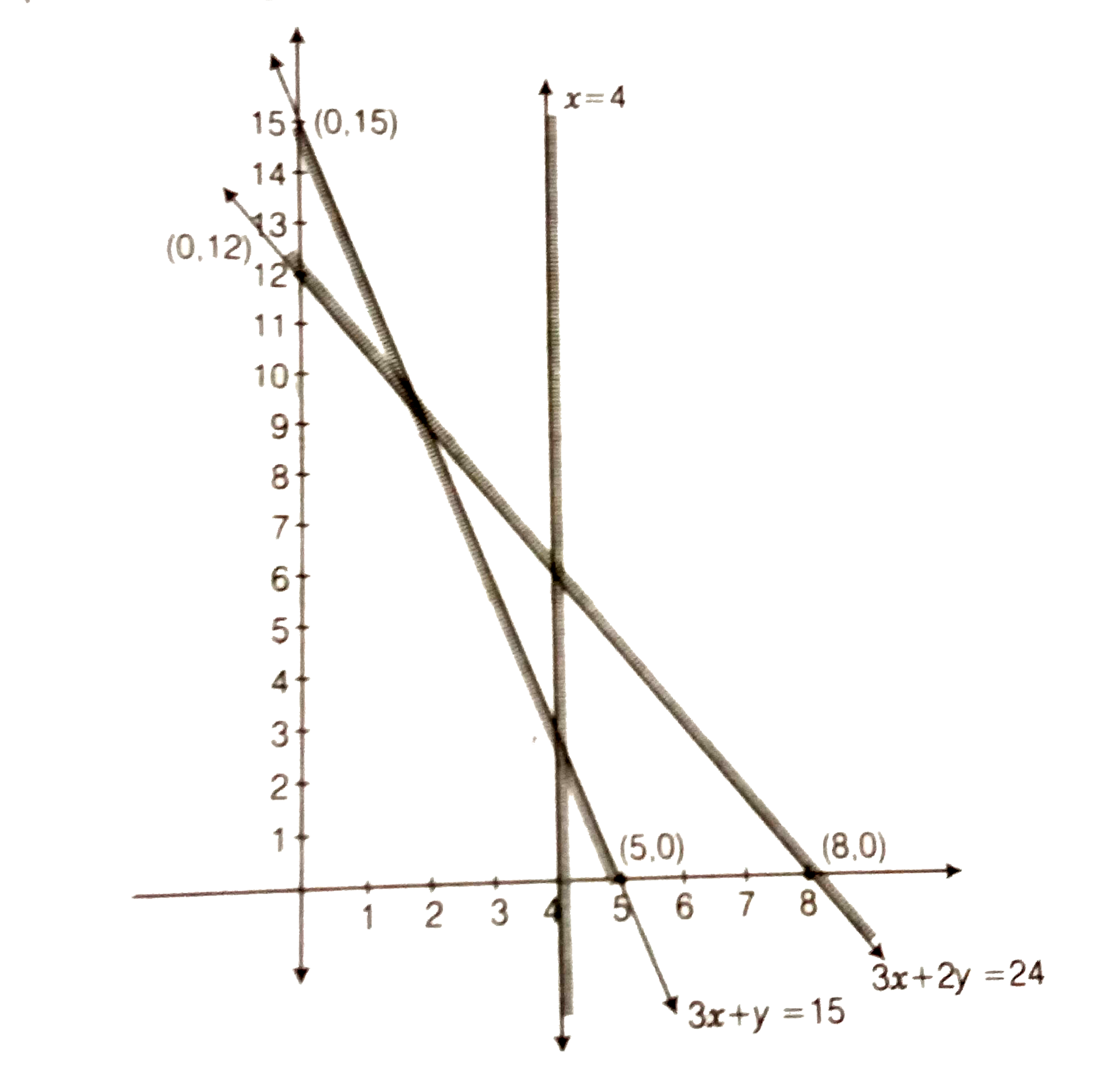
It is clear from the graph that there is no common region corresponding to these inequality.
Hence, the given system of inequalities have no solution.
|
Topper's Solved these Questions
- LINEAR INEQUALITIESBook:NCERT EXEMPLARChapter:LINEAR INEQUALITIESExercise:Objective Type Questions
Explore 14 Videos
- LINEAR INEQUALITIESBook:NCERT EXEMPLARChapter:LINEAR INEQUALITIESExercise:Objective Type Questions
Explore 14 Videos
- LIMITS AND DERIVATIVES Book:NCERT EXEMPLARChapter:LIMITS AND DERIVATIVES Exercise:FILLERS
Explore 4 Videos
- MATHEMATICAL REASONING Book:NCERT EXEMPLARChapter:MATHEMATICAL REASONING Exercise:OBJECTIVE TYPE QUESTIONS
Explore 21 Videos
Similar Questions
Knowledge Check
The graphical solution of the system of linear inequalities 3x,4y≥12,y≥1,x≥0 is
A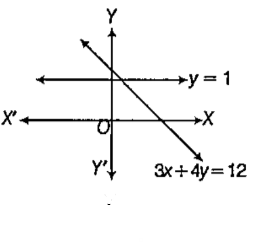 B
B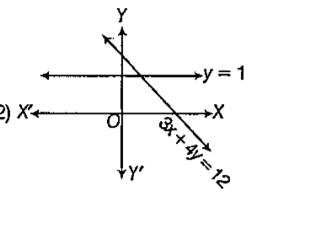 C
C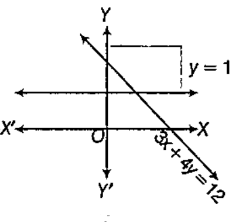 D
D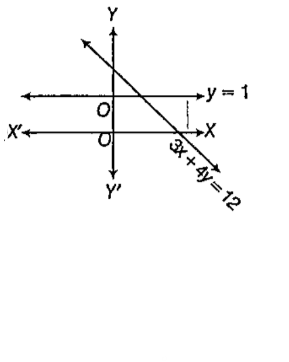
the corner points of the feasible region of a system of linear inequalities 3x+5y≤15,5x+2y≥10,x≥0,y≥0, are:
A(2,0),(2019,4519),(0,3)B(0,3),(2019,4519),(0,5)C(2,0),(2019,4519),(5,0)D(0,0),(2,0),(2019,4519),(0,3)Solve the system of linear inequations: x+2y≤10,2x+y≤8.
ALines meet at E(2,4)BLines meet at E(-2,4)CLines meet at E(2,-4)DLines meet at E(-2,-4)
Solve the following system of inequalities graphically:
x+y≤200,x≤20,y≥4x,x≥0,y≥0.
View SolutionShow that the following system of linear inequalities has no solution x+2y≤3,3x+4y≥12,x≥0,y≥1.
View SolutionSolve the following systems of inequalities for all ξnR
|2x−3|≤11,|x−2|≥3
View SolutionShow that the solution set of the following system of linear inequalities is an unbounded region 2x+y≥8,x+2y≥10,x≥0,y≥0.
View SolutionSolve the following system of inequtions graphically.
x+3y≤12,33x+y≤12,x≥0,y≥0
View Solution