If x<5, then
−x<−5
−x≤−5
−x>−5
−x≥−5
The correct Answer is:C
If x<5, then −x>−5
[if we multiply by negative numbers, then inequality get reversed]
Topper's Solved these Questions
- BOOK - NCERT EXEMPLARCHAPTER - LINEAR INEQUALITIESEXERCISE - Long Answer Type Question6videos
LINEAR INEQUALITIES
- BOOK - NCERT EXEMPLARCHAPTER - LIMITS AND DERIVATIVES EXERCISE - FILLERS4videos
LIMITS AND DERIVATIVES
- BOOK - NCERT EXEMPLARCHAPTER - MATHEMATICAL REASONING EXERCISE - OBJECTIVE TYPE QUESTIONS21videos
MATHEMATICAL REASONING
Similar Questions
If 0<logex<√x for all x<1, then find the value of limx→∞logexx.
View SolutionState which of the following statements is true of false.
(i) If x<yandb<0, then xb<yb.
(ii) If xy>0, then x>0andy<0
(iii) If xy>0, then x<0andy<0
(iv) If xy<0, then x<0andy<0
(v) If x<−5andx<−2, than x∈(−∞,−5)
(vi) If x<−5andx>2, then x∈(−5,2)
(vii) If x>−2andx<9,then x∈(−2,9)
(viii) If |x|>5, then x∈(−∞,−5)∪[5,∞)
(ix) If |x|≤4, then x∈[−4,4]
(x)Graph of x<3is
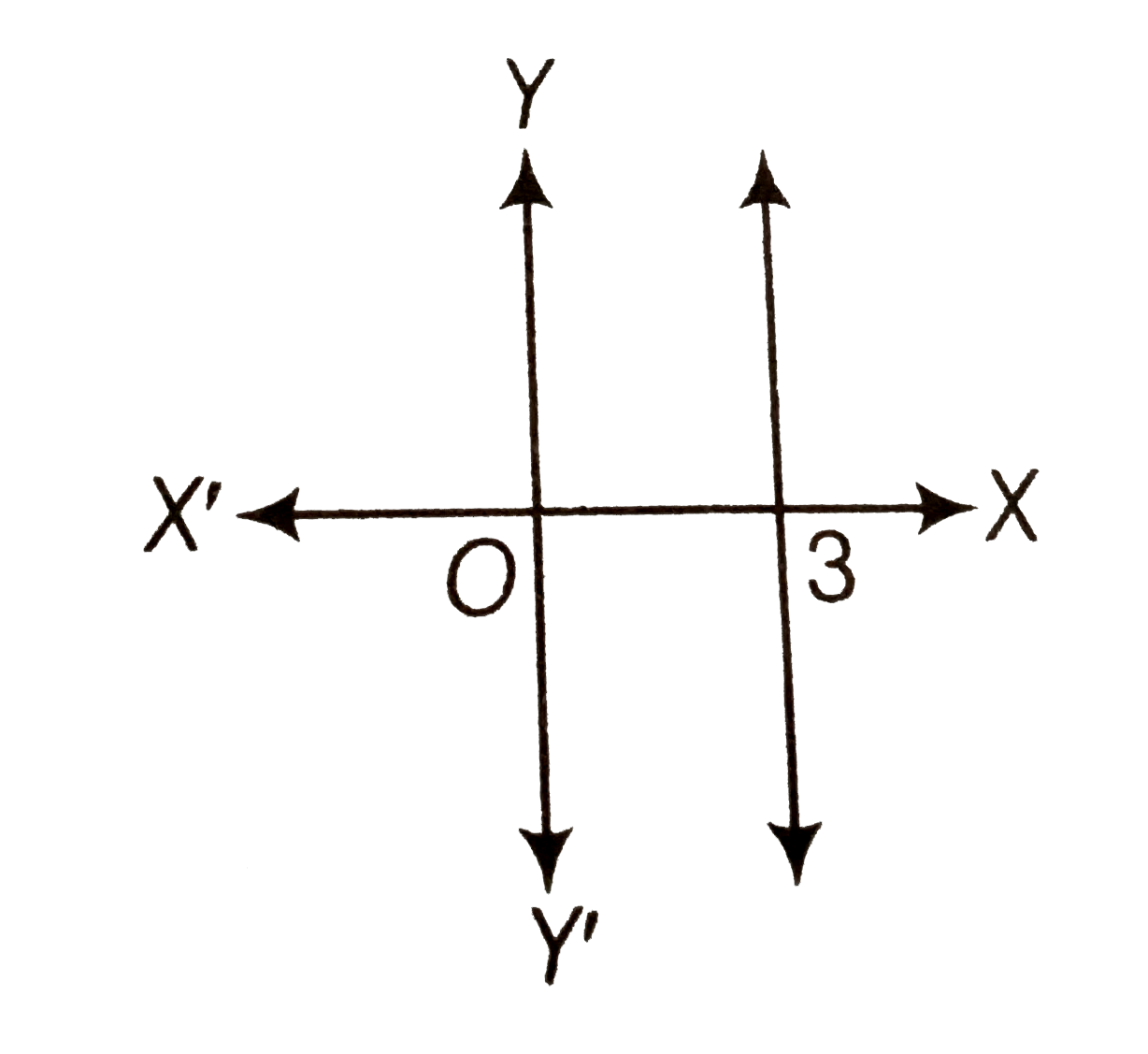
(xi) Graph of x≥0 is

(xii) Graph of y≤0 is
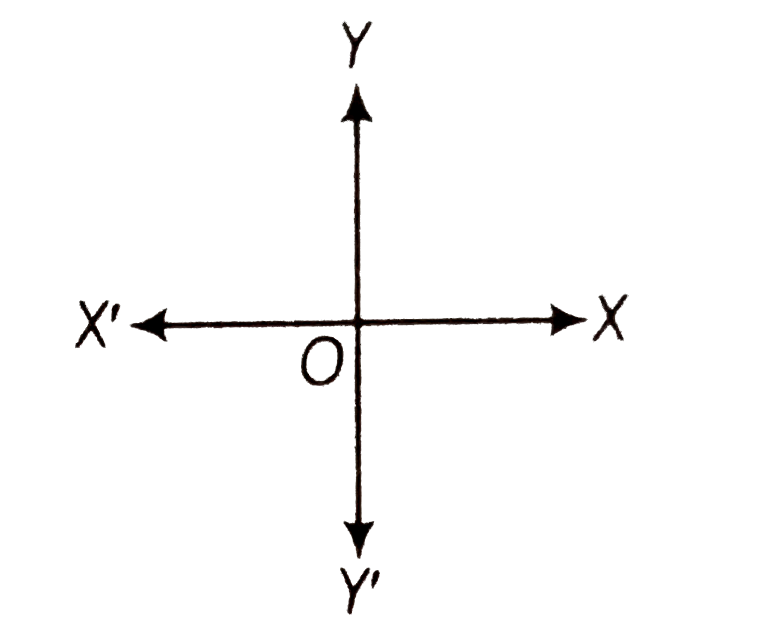
(xiii) Solution set of x≤0andy≤0 is

(xiv) Solution set of x≥0andy≤1 is
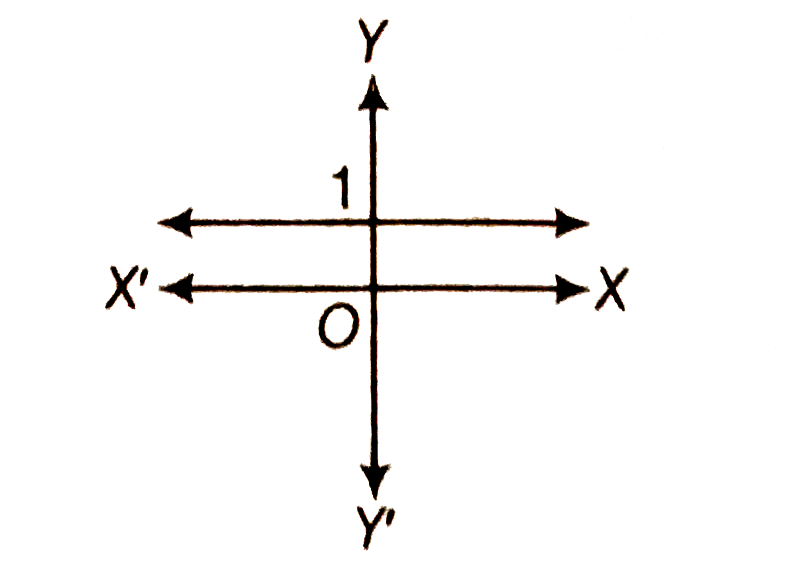
(xv) Solution set of x+y≥0 is
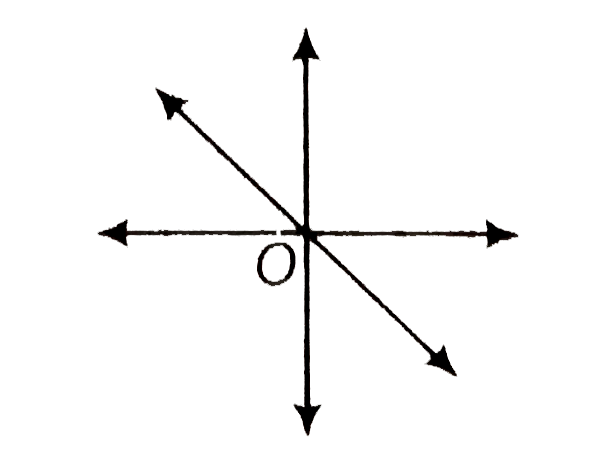 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If x<0, then value of tan−1(x)+tan−1(1x) is equal to
Aπ2B−π2C0D−π - Question 2 - Select One
if f(x) ={xfor x≥0−xfor x<0then
Af(x) is continuous at x =0 but not differentiableBf(x) is continuous and differentiable at x=0Cf(x) is differentiable at x=0Df(x) is not continuous at x=0 - Question 3 - Select One
If f(x) {xfor x≥0−xfor x<0then f(x) at x=0 is
Acontinuous but not differentiableBnot continuous but differentbaleCcontinuous and differentiableDnot continous and not differentiable
Solve 5x<24 when (i)x∈N,(ii)x∈Z.
In each, case, represent the solution set on the number line.View SolutionIf y=x+x2+x3+.... up to infinite terms where x<1, then which one of the following is correct?
View SolutionIf A={x:x∈W,x≤8} and B={x:x∈W,x<19}, the n(A−B)=____.
View SolutionIf (log3x)2+log3x<2, then which one of the following is correct ?
View SolutionIf f(x) =⎧⎪⎨⎪⎩x+2for −2<x<35for x=38−xforx>3,then at x=3 ,f'(x) =
View Solution

