The points whose abscissa and ordinate have different signs will lie in
I and II quadrants
II and III quadrants
I and III quadrants
II and IV quadrants
The correct Answer is:D
The points whose abscissa and ordinate have different signs will be of the form (-x,y) or (x,-y) and these points will lie in II and IV quadrants.
Topper's Solved these Questions
Similar Questions
5) If a point P(2,3) lies in first quadrant then what will be the coordinates of point Q opposite to it in fourth quadrant having equal distant from both the axes 6) In the fig. given below, name the point whose abscissa and ordinate both are positive and write the abscissa and ordinate of the point E:
View SolutionA point whose abscissa and ordinate are 2 and −5 respectively, lies in (a) First quadrant (b) Second quadrant (c) Third quadrant (d) Fourth quadrant
View Solution
Knowledge Check
The point whose abscissa and ordinate have different signs will lie in
AI and II quadrantsBI and III quadrantsCII and III quadrantsDII and IV quadrantIf abscissa of a point is zero then that point will lie
Aon x-axisBon y-axisCat originDin 1st quadrantThe point whose abscissa is equal to its ordinate and which is equidistant from A(−1,0) and B(0,5) is
A(1, 1)B(2, 2)C(-2, -2)D(3, 3)
In the fig. given below, name whose abscissa and ordinate both are positive and write the abscissa and ordinate of the point E.
View SolutionFrom the given figure, answer the following questions
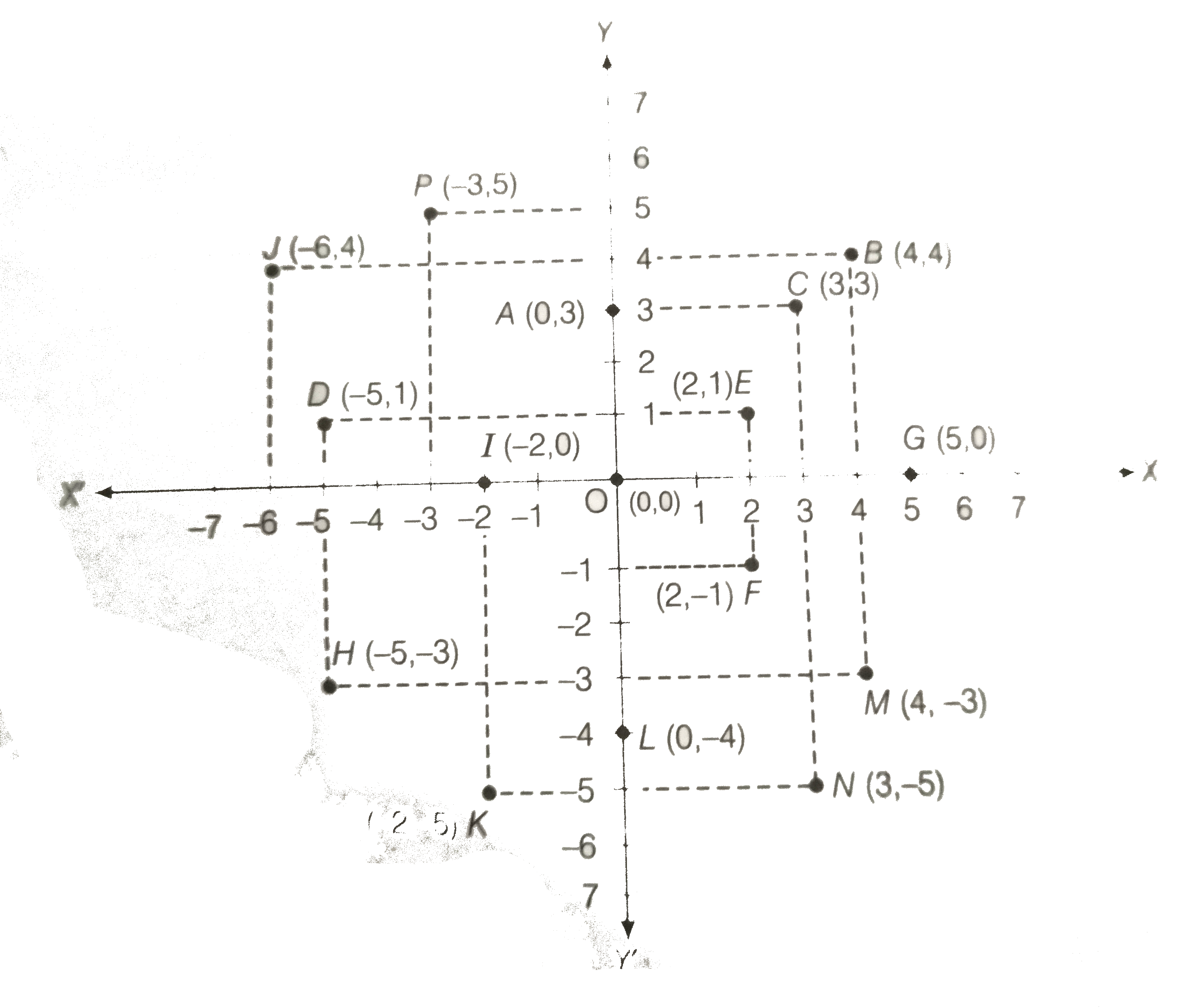
(i) Write the points whose abscissa is 0.
(ii) Write the points whose ordinate is 0.
(iii) Write the points whose abscissa is -5.
View SolutionA point whose abscissa is −3 and ordinate 2 lies in (a) First quadrant (b) Second quadrant (c) Third quadrant (d) Fourth quadrant
View SolutionTwo points having same abscissae but different ordinates lie on (a) x-a xi s (b) y-a xi s (c) a line parallel to y-a xi s (d) a line parallel to x-a xi s
View SolutionIf the curve xy=R2−16 represents a rectangular hyperbola whose branches lies only in the quadrant in which abscissa & ordinate are possite in sign but not equal in magnitude, then
View Solution
