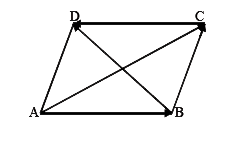
Figure shows a parallelogram ABCD. Prove that −−→AC+−−→BD=2−−→BC'
Video Solution
Text Solution
The correct Answer is:2−−→BC
−−→AC=−−→AB+−−→BC
−−→BD=−−→BC+−−→CD [applying triangle law of vectors]
Now −−→AC+−−→BD=−−→AB+−−→BC+−−→BC+−−→CD=−−→AB+2−−→BC+−−→CD
But −−→CD=−−−→AB∴−−→AC+−−→BD=−−→AB+2−−→BC−−−→AB=2−−→BC
|
Similar Questions
Knowledge Check
If ABCD is a parallelogram, then −−→AC−−−→BD=
A4−−→ABB3−−→ABC2−−→ABD−−→ABE and F are the interior points on the sides BC and CD of a parallelogram ABCD. Let −−→BE=4−−→ECand−−→CF=4−−→FD. If the line EF meets the diagonal AC in G, then −−→AG=λ−−→AC, where λ is equal to :
A13B2125C713D215E and F are the interior points on the sides BC and CD of a parallelogram ABCD. Let −−→BE=4−−→ECand−−→CF=4−−→FD. If the line EF meets the diagonal AC in G, then −−→AG=λ−−→AC, where λ is equal to :
A13B2125C713D215
The given figure shows a quadrilateral ABCD. Prove that :
AB+BC+CD+DA>AC+BD

View SolutionABCD is a parallelogram and AC, BD are its diagonals. Show that :
−−→AC+−−→BD=2−−→BC,−−→AC−−−→BD=2−−→AB.
View SolutionIf →aand→b represent two adjacent sides →ABand→BC respectively of a parallelogram ABCD, then show that its diagonals →ACand→DB are equal to →a+→b and →a−→b respectively.
View SolutionABCD is a parallelogram Fig. 2 (c ) .64. ACand(BD)areitsdiagonals.Showtˆ<br> (a) vec (AC) +vec (BD) =2 vec (BC)<br>(b)vec (AC) - vec (BD) =2 vec (AB)
 .
.
View SolutionABCD is a parallelogram . If −−→AB=→a,−−→BC=→b, then what −−→BD equal to ?
View Solution
