एक समबाहु त्रिभुज के शीर्षो पर तीन आवेश q1,q2 और q3 जिनमे से प्रत्येक का मान q है, रखे गए है । त्रिभुज की प्रत्येक भुजा की लम्बाई l है। यदि उसके केंद्रित पर समान चिन्ह वाला आवेश Q स्थित हो , तो उस पर परिणामी बल की गणना कीजिए।
चित्र में ABC एक समबाहु त्रिभुज है, जिसके शीर्ष A ,B और C पर क्रमशः q1,q2 और q3 आवेश रखे गए है । AD⊥BC खींचे।
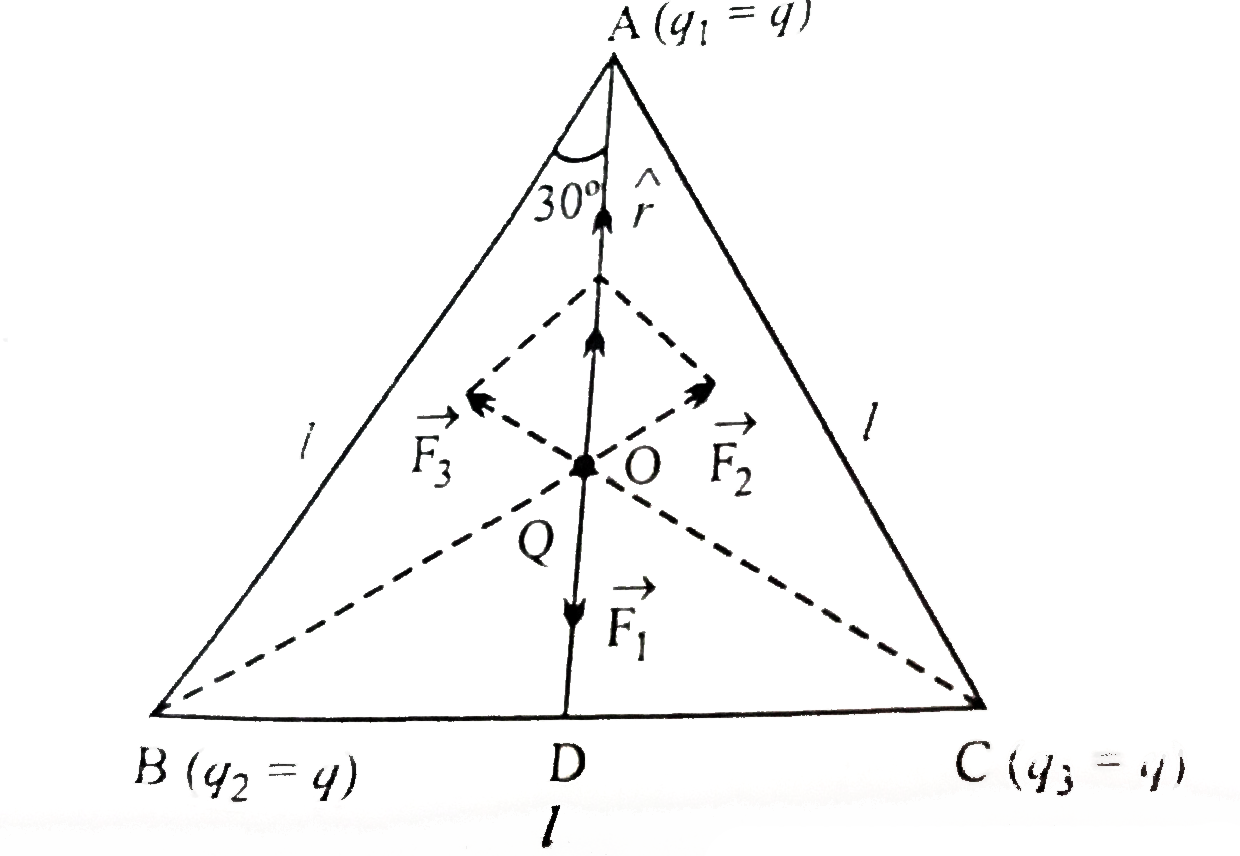
समकोण ΔADB में,
cos30∘=ADAB
∴AD=ABcos30∘=l×√32=√32l
शीर्ष A से केन्द्रक O की दुरी
OA=23AD=23×√32l=l√3
अब सममिति से OA=OB=OC
बिंदु A पर स्थित q आवेश के कारन O पर स्थित आवेश Q पर बल
F1=14πε0।=qQ(l√3)=34πε0।qQl2,AOके अनुदिश
इसी तरह बिंदु B पर स्थित आवेश q के कारण Q पर बल
F2=34πε0।qQl2,BOके अनुदिश
तथा बिंदु C पर स्थित आवेश q के कारण Q पर बल F3=34πε0।qQl2,CO के अनुदिश
चूँकि F2=F3, समांतर चतुर्भुज नियक से उनके परिणामी बल का परिमाण
F'=2F2cos(120∘2),
[∵→F2 तथा →F3 के बिच का कोण 120∘ है।]
=2×34πε0।qQl2×12
F'=34πε0।qQl2,OA के अनुदिश
अतः आवेश Q पर कुल बल
F=F'+F1
=34πε0।qQl2ˆr−34πε0।qQl2ˆr
जहाँˆr,OA के अनुदिश एकांक सदिश है ।
∴F=0.
Topper's Solved these Questions
- वैधुत आवेश और क्षेत्र Book:NAVBODHChapter:वैधुत आवेश और क्षेत्र Exercise:आंकिक उदाहरण
Explore 50 Videos
- वैधुत आवेश और क्षेत्र Book:NAVBODHChapter:वैधुत आवेश और क्षेत्र Exercise:आंकिक उदाहरण प्लस
Explore 8 Videos
- वैद्युत आवेश तथा क्षेत्रBook:NAVBODHChapter:वैद्युत आवेश तथा क्षेत्रExercise:तथ्यात्मक प्रश्न
Explore 12 Videos
- संचार व्यवस्था Book:NAVBODHChapter:संचार व्यवस्था Exercise:NCERT पाठ्य पुस्तक के प्रश्नोत्तर
Explore 9 Videos
Similar Questions
एक चालक पर 14⋅4×10−19 कूलॉम धनावेश है । इस चालाक पर कितने इलेक्ट्रॉनों की अधिकता या कमी है ?
View Solutionप्रत्येक 4μC के अनंत आवेश X -अक्ष के अनुदिश x=1 मीटर, x=2 मीटर, x=4 मीटर, x=8 मीटर दूरियों पर स्थित है। मिलबिंदु पर रखे 1 कूलॉम आवेश पर कुल बल कि गणना कीजिए।
View Solutionसामान्य विधूतरोधी होता है , किन्तु वायुयान के रबर टायर कुछ चालक बनाये जाते है , क्यों ?
View Solutionव्योम तरंगो के उपयोग द्वारा क्षितिज के पार संचार के लिए निम्नलिखित अवृत्तयियो में से कोण -सी आवृतिया उपयुक्त रहेगी -
View Solutionबिंदु P,Q,R,S के निर्देशांक (2,a),(3,5),(3,4)और (0,6) है । यदि रेखा PR लंबवत हो QS पर तो a का मान ज्ञात कीजिए ।
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionएक छड़ की लम्बाई l है । इसका एक सिरा भूमि पर तथा दूसरा सिरा एक ऊर्ध्वाधर दीवार पर टिका है । यदि छड़ भूमि पर फिसले , तो उसके मध्य बिंदु का बिन्दुपथ ज्ञात कीजिए ।
View Solutionएक परवलय के नाभिलम्ब का समीकरण x+y=8 तथा उसके शीर्ष पर स्पर्शी का समीकरण x+y=12 है, तो उसके नाभिलम्ब की लम्बाई है :
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionएक समबाहु त्रिभुज की भुजाएँ 2 सेमी/से की दर से बढ़ रही है। क्षेत्रफल के बढ़ने की दर, जबकि भुजा 10 सेमी हो, है
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 36∘ का कोण बनाती है| बहुभुज की भुजाओं की संख्या ज्ञात कीजिए |
View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 45∘ का कोण बनाती है| बहुभुज का नाम दीजिए |
View Solutionएक बिंदु P, x-अक्ष पर और एक अन्य बिंदु Q, y-अक्ष पर स्थित है। (i) बिंदु P की कोटि ज्ञात कीजिए।
View Solutionएक बिन्दु पर क्रियाशील दो बल P और Q का अधिकतम परिणामी बल ........ होता है।
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solution