Question

The curve for the moment of inertia of a sphere of constant mass M versus its radius will be:

Options

A.
B.
C.
D.

Answer

A

Explanation

To determine the curve for the moment of inertia of a sphere of constant mass $$M$$ versus its radius $$r$$, we can follow these steps:

Step 1: Understand the Formula for Moment of Inertia
The moment of inertia \( I \) of a solid sphere about an axis through its center is given by the formula:
\( I = \frac{2}{5} M r^2 \)
where \( M \) is the mass of the sphere and \( r \) is its radius.

Step 2: Identify the Variables
In this scenario, we have:
- Mass \( M \) is constant.
- Radius \( r \) is the variable.

Step 3: Express Moment of Inertia in Terms of Radius
Since \( M \) is constant, we can express the moment of inertia as:
\( I = k r^2 \)
where \( k = \frac{2}{5} M \) is a constant.

Step 4: Analyze the Relationship
The equation \( I = k r^2 \) is a quadratic equation in terms of \( r \). This indicates that the moment of inertia \( I \) is proportional to the square of the radius \( r \).

Step 5: Graph the Relationship
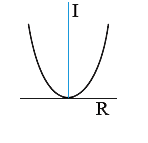
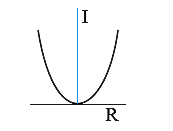
When plotting \( I \) (y-axis) against \( r \) (x-axis), the graph will be a parabola opening upwards, starting from the origin (0,0) since when \( r = 0 \), \( I \) will also be 0.

Step 6: Conclusion
Thus, the curve for the moment of inertia of a sphere of constant mass \( M \) versus its radius \( r \) will be a parabola that passes through the origin.

Final Answer
The correct answer is that the graph will be a parabola.

---