The relation between angular momentum J of a body and rotational kinetic energy is given by . The graph between J and will be:

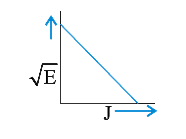

The correct Answer is:A
To solve the problem, we need to analyze the relationship between angular momentum J and rotational kinetic energy E given by the equation:
J=√2EI
Step 1: Rearranging the Equation
We can express the equation in a more useful form for graphing. Squaring both sides gives:
J2=2EI
Step 2: Expressing Energy in Terms of J
From the equation J2=2EI, we can express E in terms of J:
E=J22I
Step 3: Identifying the Variables
In this equation:
- J is on the y-axis (dependent variable).
- E is on the x-axis (independent variable).
- The constant 12I acts as the slope of the line when we plot E against J2.
Step 4: Analyzing the Graph
The equation E=12IJ2 represents a quadratic relationship between E and J. However, since we want to plot J against √E, we need to express J in terms of √E.
Step 5: Expressing J in Terms of sqrt(E)
Taking the square root of both sides of the rearranged equation gives:
J=√2I⋅√E
Step 6: Graph Characteristics
This equation J=√2I⋅√E indicates that:
- The graph will be a straight line.
- It passes through the origin because when E=0, J will also be 0.
- The slope of the line is √2I.
Conclusion
The graph between J and √E will be a straight line passing through the origin.
We can express the equation in a more useful form for graphing. Squaring both sides gives:
From the equation J2=2EI, we can express E in terms of J:
In this equation:
- J is on the y-axis (dependent variable).
- E is on the x-axis (independent variable).
- The constant 12I acts as the slope of the line when we plot E against J2.
The equation E=12IJ2 represents a quadratic relationship between E and J. However, since we want to plot J against √E, we need to express J in terms of √E.
Taking the square root of both sides of the rearranged equation gives:
This equation J=√2I⋅√E indicates that:
- The graph will be a straight line.
- It passes through the origin because when E=0, J will also be 0.
- The slope of the line is √2I.
The graph between J and √E will be a straight line passing through the origin.
Similar Questions
Knowledge Check
Relationship between angular momentum L and kinetic energy E of a rigid body in pure rotation is
AE=L2/2IBE2=2I/LCL=E2/2IDE = 2ILThe relation between kinetic energy K and linear momentum p of a particle is represented by
AK2=2mpB2K2=mpCp2=2mkD2mK=pThe relation between kinetic energy K and linear momentum p of a particle is represented by
AK2=2mpB2K2=mpCp2=2mKD2mK=p
Find the momentum of a body of mass 100 g having a kinetic energy of 20 J.
View SolutionEstablish a relation between angular momentum and moment of inertia of a rigid body.
View SolutionDerive the relation between kinetic energy and moment of inertia of a body in rotation motion.
View SolutionThe momentum of a body of mass 200g with kinetic energy of 10 J is:
View SolutionThe graph between the angular momentum J and angular velocity ω will be :-
View Solution