A body of mass 60 kg is holding a vertical rope . The rope can break when a mass of 75 kg is suspended from it. The maximum acceleration with which the boy can climb the rope without breaking it is :(g=10m/s2)
2.5m/s2
5.0m/s2
7.5m/s2
22.5m/s2
The correct Answer is:1
To find the maximum acceleration with which the boy can climb the rope without breaking it, we can follow these steps:
Step 1: Identify the forces acting on the boy
The forces acting on the boy (mass m=60kg) are:
- The gravitational force acting downward, which is Fg=m⋅g=60kg⋅10m/s2=600N.
- The tension T in the rope acting upward.
Step 2: Determine the maximum tension in the rope
The rope can break when a mass of 75kg is suspended from it. The maximum tension Tmax that the rope can withstand is given by the weight of this mass:
Tmax=75kg⋅10m/s2=750N
Step 3: Apply Newton's second law
When the boy climbs the rope with an acceleration a, the net force acting on him can be expressed using Newton's second law:
T−Fg=m⋅a
Substituting the values we have:
T−600N=60kg⋅a
Step 4: Substitute the maximum tension into the equation
We know that the maximum tension T cannot exceed 750N. Therefore, we set T=Tmax:
750N−600N=60kg⋅a
150N=60kg⋅a
Step 5: Solve for the acceleration a
Now, we can solve for a:
a=150N60kg=2.5m/s2
Final Answer
The maximum acceleration with which the boy can climb the rope without breaking it is 2.5m/s2.
---
The forces acting on the boy (mass m=60kg) are:
- The gravitational force acting downward, which is Fg=m⋅g=60kg⋅10m/s2=600N.
- The tension T in the rope acting upward.
The rope can break when a mass of 75kg is suspended from it. The maximum tension Tmax that the rope can withstand is given by the weight of this mass:
Tmax=75kg⋅10m/s2=750N
When the boy climbs the rope with an acceleration a, the net force acting on him can be expressed using Newton's second law:
T−Fg=m⋅a
Substituting the values we have:
T−600N=60kg⋅a
We know that the maximum tension T cannot exceed 750N. Therefore, we set T=Tmax:
750N−600N=60kg⋅a
150N=60kg⋅a
Now, we can solve for a:
a=150N60kg=2.5m/s2
The maximum acceleration with which the boy can climb the rope without breaking it is 2.5m/s2.
Similar Questions
A 50 kg man stuck in flood is being lifted vertically by an army helicopter with the help of light rope which can bear a maximum tension of 70 kg-wt. The maximum acceleration with which helicopter can rise so that rope does not breaks is (g=9.8ms−2)
View SolutionThe maximum tension a rope can withstand is 60 kg - wt. The ratio of maximum acceleration with which two boys of masses 20kg and 30kg can climb up the rope at the same time is
View Solution
Knowledge Check
A monkey of mass 20kg is holding a vertical rope. The rope will not break when a mass of 25kg is suspended from it but will break it the mass exeeds 25kg . What is the maximum acceleration with which the monkey can climb up along the rope? (g=10m/s2) .
A10m/s2B25m/s2C2.5m/s2D5m/s2A monkey of 25 kg is holding a vertical rope. The rope does not break if a body of mass 30 kg is suspended with the rope exceeds 30 kg. What will be the maximum acceleration with which the monkey can climb up along the rope ? ( Take ,=10ms−2)
A2ms−2B2.5ms−2C3ms−2D4ms−2A body of mass 40 kg wants to climb up a rope hanging vertically. The rope can withstands a maximum tension of 500 N. What is the maximum acceleration with which the boy can climb rope? Tak e g=10m/s2
A1.5m/s2B2.0m/s2C2.5m/s2D3.0m/s2
The maximum tension a rope can withstand is 60kg−wt The ratio of maximum accelertion with which two boys of masses 20kg and 3kg can climb up the rope at the same time is .
View SolutionThe minimum acceleration with which a fireman can slide down a rope of breaking strength two - third of his weight is
View SolutionA 50 kg man stuck in flood is being lifted vertically by an army helicopter with the help of light rope which can bear a maximum tension of 70 kg-wt. The maximum acceleration with which helicopter can rise so that rope does not breaks is (g=9.8ms−2)
View SolutionBlock B of mass 100 kg rests on a rough surface of friction coeffcient μ=1/3. A rope is tied to block B as shown in figure. The maximum acceleration with which boy A of 24 kg can climbs on rope without making block move is :
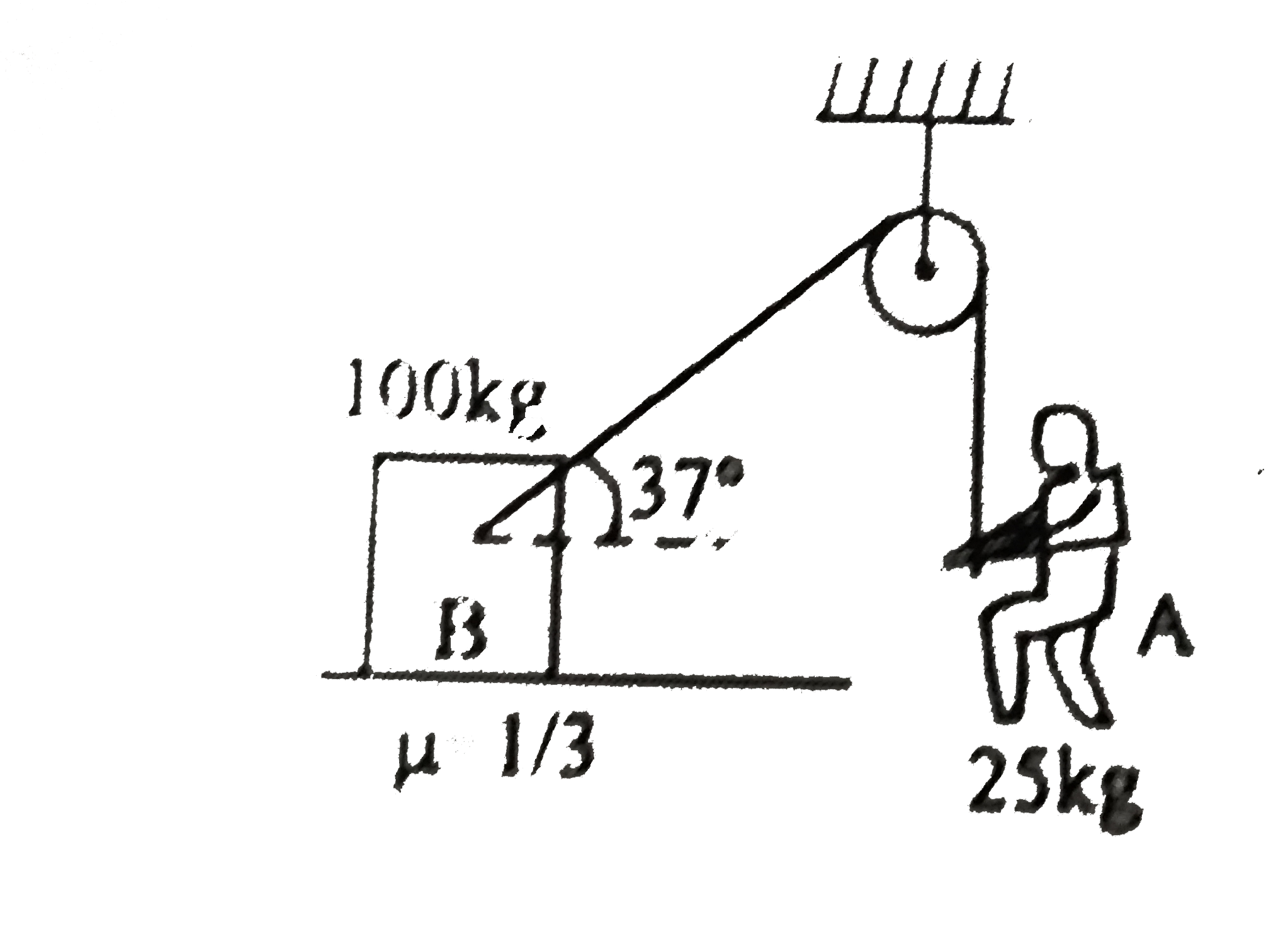
View SolutionA monkey of mass 30 kg climbs a rope which can withstand a maximum tension of 360 N. The maximum acceleration which this rope can tolerate for the climbing of monkey is:
(g=10m/s2)
View Solution

