The maximum tension a rope can withstand is 60kg−wt The ratio of maximum accelertion with which two boys of masses 20kg and 3kg can climb up the rope at the same time is .
To solve the problem, we need to analyze the forces acting on both boys as they climb the rope. The maximum tension that the rope can withstand is given as 60 kg-wt. We will convert this to Newtons for our calculations.
Step 1: Convert maximum tension to Newtons
The weight of an object in Newtons can be calculated using the formula:
Weight (N)=mass (kg)×g
where g (acceleration due to gravity) is approximately 9.8m/s2.
For 60 kg-wt:
Maximum Tension=60kg×9.8m/s2=588N
Step 2: Analyze the forces on each boy
Let’s denote:
- Mass of boy 1 (m1) = 20 kg
- Mass of boy 2 (m2) = 3 kg
For each boy climbing up, the forces acting on them are:
1. The upward force due to tension in the rope (T).
2. The downward force due to their weight (mg).
The net force (F_net) acting on each boy can be expressed as:
Fnet=T−mg
Using Newton’s second law, we can relate the net force to acceleration (a):
Fnet=ma
Step 3: Set up equations for both boys
For boy 1 (20 kg):
T−(20kg×9.8m/s2)=20kg⋅a1
T−196=20a1(1)
For boy 2 (3 kg):
T−(3kg×9.8m/s2)=3kg⋅a2
T−29.4=3a2(2)
Step 4: Solve for Tension (T)
From equations (1) and (2), we can express T in terms of a1 and a2:
From (1):
T=20a1+196
From (2):
T=3a2+29.4
Setting both expressions for T equal to each other:
20a1+196=3a2+29.4
Step 5: Rearranging the equation
Rearranging gives:
20a1−3a2=29.4−196
20a1−3a2=−166.6(3)
Step 6: Maximum Tension Condition
Since the maximum tension T can be 588 N, we can substitute T into either equation (1) or (2) to find the maximum accelerations a1 and a2.
Using equation (1) with T = 588 N:
588=20a1+196
20a1=588−196
20a1=392
a1=39220=19.6m/s2
Now using equation (2) with T = 588 N:
588=3a2+29.4
3a2=588−29.4
3a2=558.6
a2=558.63=186.2m/s2
Step 7: Find the ratio of maximum accelerations
Now we can find the ratio of maximum accelerations a1a2:
a1a2=19.6186.2
Final Calculation
Calculating the ratio:
a1a2≈0.105
Conclusion
The ratio of maximum acceleration with which the two boys can climb up the rope at the same time is approximately 0.105.
The weight of an object in Newtons can be calculated using the formula:
Weight (N)=mass (kg)×g
where g (acceleration due to gravity) is approximately 9.8m/s2.
Maximum Tension=60kg×9.8m/s2=588N
Let’s denote:
- Mass of boy 1 (m1) = 20 kg
- Mass of boy 2 (m2) = 3 kg
1. The upward force due to tension in the rope (T).
2. The downward force due to their weight (mg).
Fnet=T−mg
Fnet=ma
For boy 1 (20 kg):
T−(20kg×9.8m/s2)=20kg⋅a1
T−196=20a1(1)
T−(3kg×9.8m/s2)=3kg⋅a2
T−29.4=3a2(2)
From equations (1) and (2), we can express T in terms of a1 and a2:
From (1):
T=20a1+196
From (2):
T=3a2+29.4
20a1+196=3a2+29.4
Rearranging gives:
20a1−3a2=29.4−196
20a1−3a2=−166.6(3)
Since the maximum tension T can be 588 N, we can substitute T into either equation (1) or (2) to find the maximum accelerations a1 and a2.
588=20a1+196
20a1=588−196
20a1=392
a1=39220=19.6m/s2
588=3a2+29.4
3a2=588−29.4
3a2=558.6
a2=558.63=186.2m/s2
Now we can find the ratio of maximum accelerations a1a2:
a1a2=19.6186.2
Calculating the ratio:
a1a2≈0.105
The ratio of maximum acceleration with which the two boys can climb up the rope at the same time is approximately 0.105.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:C.U.Q
Explore 73 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -I (C.W)
Explore 47 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - IV
Explore 41 Videos
Similar Questions
The maximum tension a rope can withstand is 60 kg - wt. The ratio of maximum acceleration with which two boys of masses 20kg and 30kg can climb up the rope at the same time is
View SolutionA 50 kg man stuck in flood is being lifted vertically by an army helicopter with the help of light rope which can bear a maximum tension of 70 kg-wt. The maximum acceleration with which helicopter can rise so that rope does not breaks is (g=9.8ms−2)
View Solution
Knowledge Check
A body of mass 40 kg wants to climb up a rope hanging vertically. The rope can withstands a maximum tension of 500 N. What is the maximum acceleration with which the boy can climb rope? Tak e g=10m/s2
A1.5m/s2B2.0m/s2C2.5m/s2D3.0m/s2A body of mass 60 kg is holding a vertical rope . The rope can break when a mass of 75 kg is suspended from it. The maximum acceleration with which the boy can climb the rope without breaking it is :(g=10m/s2)
A2.5m/s2B5.0m/s2C7.5m/s2D22.5m/s2A monkey of 25 kg is holding a vertical rope. The rope does not break if a body of mass 30 kg is suspended with the rope exceeds 30 kg. What will be the maximum acceleration with which the monkey can climb up along the rope ? ( Take ,=10ms−2)
A2ms−2B2.5ms−2C3ms−2D4ms−2
Block B of mass 100 kg rests on a rough surface of friction coeffcient μ=1/3. A rope is tied to block B as shown in figure. The maximum acceleration with which boy A of 24 kg can climbs on rope without making block move is :
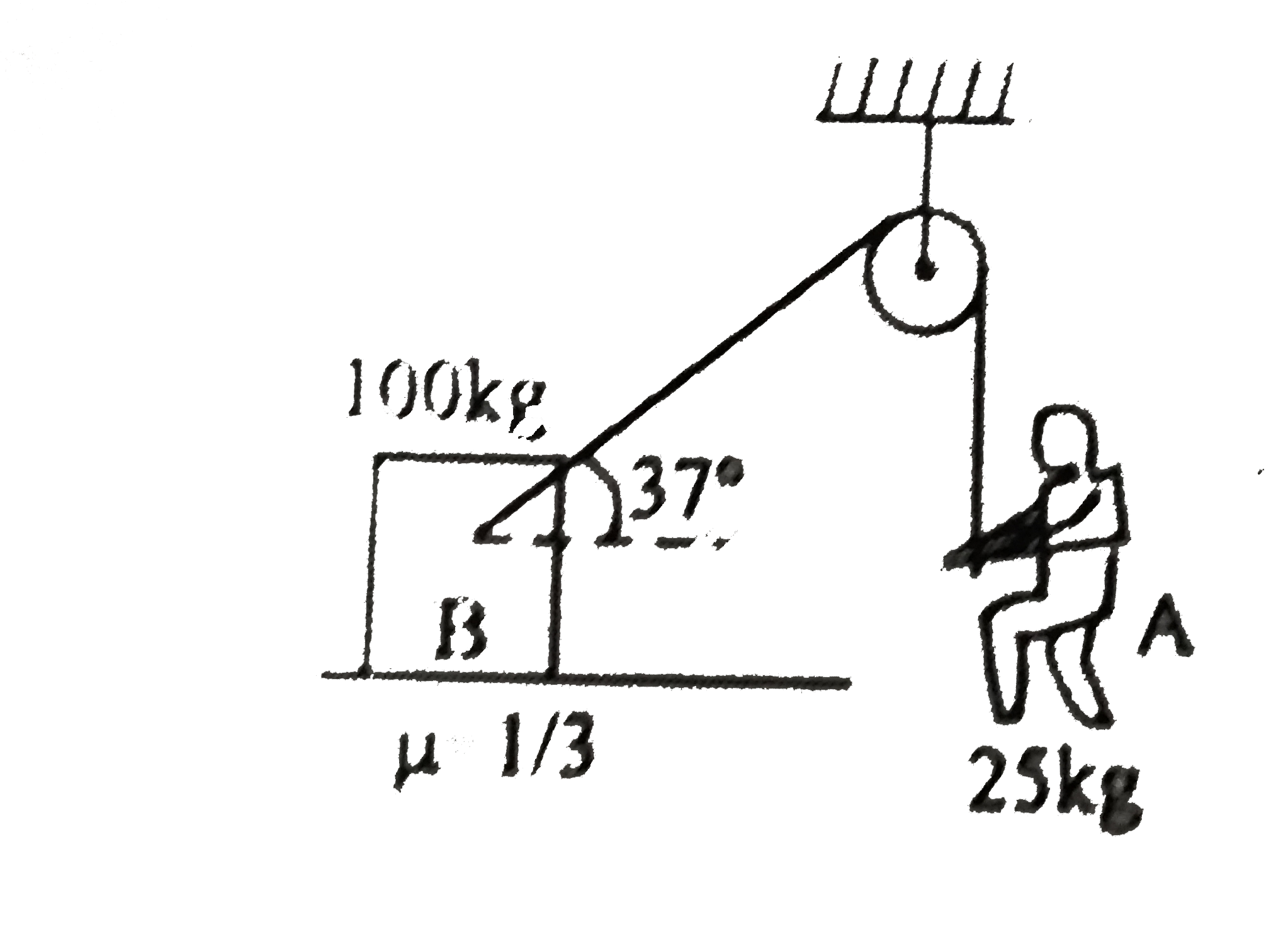
View SolutionA 24 kg block resting on a floor has a rope tied to its top. The maximum tension , the rope can withstand without breaking is 310 N . The minimum time in which the block can be lifted a vertical distance of 4.6 m by pulling on the rope is
View SolutionA monkey of mass 30 kg climbs a rope which can withstand a maximum tension of 360 N. The maximum acceleration which this rope can tolerate for the climbing of monkey is:
(g=10m/s2)
View SolutionOne end of a massless rope, which passes over a massless and frictionless pulley P is tied to a hook C while the other end is free. Maximum tension that the rope can bear is 360 N. With what value of maximum safe acceleration (in ms−2) can a man of 60kg climb down the rope?

View SolutionA 50 kg man stuck in flood is being lifted vertically by an army helicopter with the help of light rope which can bear a maximum tension of 70 kg-wt. The maximum acceleration with which helicopter can rise so that rope does not breaks is (g=9.8ms−2)
View Solution

