Two bodies are thrown vertically upwards with their initial velocity in the ratio 2:3. Then the ratio of the maximum height attained by them is
1:1
4:9
2:3
√2:√3
The correct Answer is:B
To solve the problem of finding the ratio of the maximum heights attained by two bodies thrown vertically upwards with their initial velocities in the ratio of 2:3, we can follow these steps:
Step 1: Understand the relationship between initial velocity and maximum height
When a body is thrown upwards, it will rise to a maximum height where its final velocity becomes zero. The relationship between the initial velocity (u), final velocity (v), acceleration due to gravity (g), and maximum height (h) can be expressed using the equation:
v2=u2−2gh
Step 2: Rearranging the equation for maximum height
At the maximum height, the final velocity v=0. Thus, we can rearrange the equation to find the maximum height:
0=u2−2gh
This simplifies to:
h=u22g
This shows that the maximum height h is directly proportional to the square of the initial velocity u.
Step 3: Define the initial velocities
Let the initial velocities of the two bodies be u1 and u2. According to the problem, the ratio of their initial velocities is given as:
u1u2=23
Step 4: Express the maximum heights in terms of initial velocities
Using the relationship derived in Step 2, the maximum heights h1 and h2 for the two bodies can be expressed as:
h1=u212g
h2=u222g
Step 5: Find the ratio of the maximum heights
To find the ratio of the maximum heights h1h2:
h1h2=u212gu222g=u21u22
Step 6: Substitute the ratio of initial velocities
Now substituting the ratio of the initial velocities:
h1h2=(u1u2)2=(23)2=49
Conclusion
Thus, the ratio of the maximum heights attained by the two bodies is:
h1h2=49
When a body is thrown upwards, it will rise to a maximum height where its final velocity becomes zero. The relationship between the initial velocity (u), final velocity (v), acceleration due to gravity (g), and maximum height (h) can be expressed using the equation:
v2=u2−2gh
At the maximum height, the final velocity v=0. Thus, we can rearrange the equation to find the maximum height:
0=u2−2gh
This simplifies to:
h=u22g
This shows that the maximum height h is directly proportional to the square of the initial velocity u.
Let the initial velocities of the two bodies be u1 and u2. According to the problem, the ratio of their initial velocities is given as:
u1u2=23
Using the relationship derived in Step 2, the maximum heights h1 and h2 for the two bodies can be expressed as:
h1=u212g
h2=u222g
To find the ratio of the maximum heights h1h2:
h1h2=u212gu222g=u21u22
Now substituting the ratio of the initial velocities:
h1h2=(u1u2)2=(23)2=49
Thus, the ratio of the maximum heights attained by the two bodies is:
h1h2=49
Similar Questions
A stone thrown vertically upwards takes 3 s to attain maximum height. Find the
(i) initial velocity of the stone
(ii) maximum height attained by the stone (g=9.8ms−2)
View SolutionTwo balls of different masses are thrown vertically upward with same initial velocity. Height attained by them are h1andh2 respectively. What is h1/h2 ?
View Solution
Knowledge Check
Two balla A and B are thrown vertically upwards with their initial velocity in the ratio 3:4.
(i) The ratio of the maximum height attained by them is 9:16
(ii) The ratio of the maximum height attained by them is 3:4
(iii) The ratio of their time taken by them to raturn back to the ground is 3:4
(iv) The ratio of their time taken by them to raturn back to the ground is 9:16A(i), (ii)B(i),(iii)C(ii),(iii)D(ii),(iv)A particle is thrown vertically upwards. If its velocity is half of the maximum height is 20m/s, then maximum height attained by it is
A25 mB30 mC35 mD40 mA body thrown vertically upwards with an initial valocity u reaches maximum height in 6 s. The ratio of the distances traveled by the body in the first second the seventh second is
A1:1B11:1C1:2D1:11
A stone is thrown vertically upwards with a velocity of 4.9ms−1. Calculate : the time taken to reach the maximum height.
View SolutionWhen a body thrown vertically up with an initial velocity vo ,then maximum height reached by the body is
View SolutionWhen a ball is thrown vertically upwards, at the maximum height
View SolutionA rocket is projected vertically upwards and its time velocity graph is shown in the figure-1.115. The maximum height attained by the rocket is :
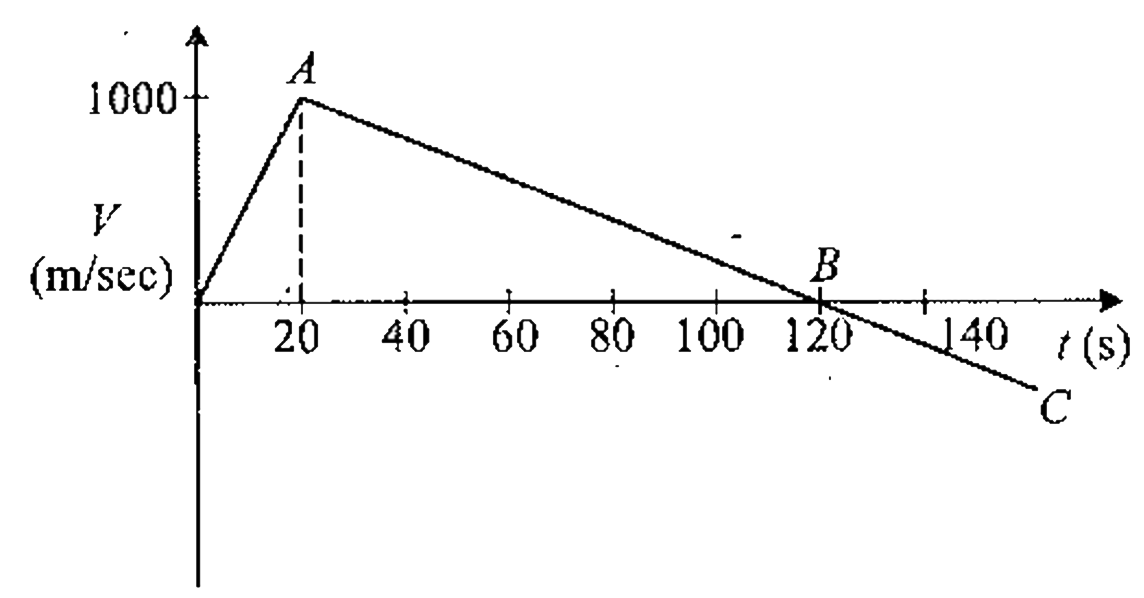
View SolutionWhen a particle is thrown vertically upwards, its velocity at one third of its maximum height is 10√2m/s. The maximum height attained by it is
View Solution

