What is the degree measure of an angle that measures 7π15 radians ?
(360−7π15)∘
(180−7π15)∘
252∘
84∘
The correct Answer is:D
To convert the angle from radians to degrees, we can follow these steps:
Step 1: Write down the given angle in radians.
The angle given is 7π15 radians.
Step 2: Use the conversion formula.
To convert radians to degrees, we use the formula:
Degrees=Radians×180π
Step 3: Substitute the given angle into the formula.
Substituting 7π15 into the formula gives:
Degrees=7π15×180π
Step 4: Simplify the expression.
Notice that π in the numerator and denominator cancels out:
Degrees=7×18015
Step 5: Calculate 18015.
Now, we simplify 18015:
18015=12
So, we have:
Degrees=7×12
Step 6: Multiply to find the degree measure.
Calculating 7×12:
Degrees=84
Final Answer:
The degree measure of the angle is 84∘.
---
The angle given is 7π15 radians.
To convert radians to degrees, we use the formula:
Degrees=Radians×180π
Substituting 7π15 into the formula gives:
Degrees=7π15×180π
Notice that π in the numerator and denominator cancels out:
Degrees=7×18015
Now, we simplify 18015:
18015=12
So, we have:
Degrees=7×12
Calculating 7×12:
Degrees=84
The degree measure of the angle is 84∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the angle measure of 4 radians ?
A114.591∘B141.372∘C229.183∘D282.743∘What is the measure in degrees of an angle that is π4 radians?
A4∘B25∘C45∘D90∘In this triangle, what is the degree measure of angle c ?
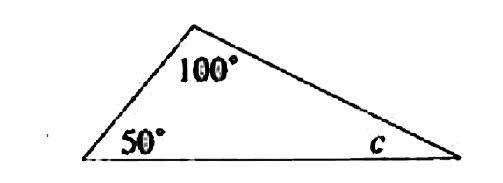 A17B20C30D40
A17B20C30D40
Find the degree measures corresponding to the radian measures:(7π6)c
View SolutionFind the degree measures corresponding to the radian measures: (4π3)c
View SolutionFind the degree measures corresponding to the radian measures: (5π3)c
View SolutionFind the degree measure corresponding to the radian measure 9π5 (Use π=227)
View SolutionFind the degree measures corresponding to the radian measures:(−5π24)c
View Solution

