In the standard (x, y) coordinate plane, the midpoint of ¯¯¯¯¯¯AB is (8, -5) and B is located at (12 , -1). If (x, y) are the coordinates of A, what is the value of x + y ?
−8
−7
−5
7
The correct Answer is:C
To solve the problem step by step, we need to find the coordinates of point A given the midpoint of segment AB and the coordinates of point B.
Step 1: Understand the midpoint formula
The midpoint M of a line segment connecting points A(x1,y1) and B(x2,y2) is given by:
M=(x1+x22,y1+y22)
In this case, we know the midpoint M is (8, -5) and the coordinates of point B are (12, -1).
Step 2: Set up the equations
Let the coordinates of point A be (x,y). According to the midpoint formula, we can set up the following equations:
1. For the x-coordinates:
x+122=8
2. For the y-coordinates:
y−12=−5
Step 3: Solve for x
From the first equation:
x+122=8
Multiply both sides by 2 to eliminate the fraction:
x+12=16
Now, subtract 12 from both sides:
x=16−12=4
Step 4: Solve for y
From the second equation:
y−12=−5
Multiply both sides by 2:
y−1=−10
Now, add 1 to both sides:
y=−10+1=−9
Step 5: Find x + y
Now that we have the coordinates of point A as (4,−9), we can find x+y:
x+y=4+(−9)=4−9=−5
Final Answer
The value of x+y is −5.
---
The midpoint M of a line segment connecting points A(x1,y1) and B(x2,y2) is given by:
M=(x1+x22,y1+y22)
In this case, we know the midpoint M is (8, -5) and the coordinates of point B are (12, -1).
Let the coordinates of point A be (x,y). According to the midpoint formula, we can set up the following equations:
1. For the x-coordinates:
x+122=8
2. For the y-coordinates:
y−12=−5
From the first equation:
x+122=8
Multiply both sides by 2 to eliminate the fraction:
x+12=16
Now, subtract 12 from both sides:
x=16−12=4
From the second equation:
y−12=−5
Multiply both sides by 2:
y−1=−10
Now, add 1 to both sides:
y=−10+1=−9
Now that we have the coordinates of point A as (4,−9), we can find x+y:
x+y=4+(−9)=4−9=−5
The value of x+y is −5.
Topper's Solved these Questions
- INTERMEDIATE ALGEBRA/COORDINATE GEOMETRYBook:ENGLISH SATChapter:INTERMEDIATE ALGEBRA/COORDINATE GEOMETRYExercise:EXERCISE
Explore 12 Videos
- IMPROVING YOUR MATH SCOREBook:ENGLISH SATChapter:IMPROVING YOUR MATH SCOREExercise:VERY CHALLENGING PROBLEMS
Explore 12 Videos
- LINEAR FUNCTIONS Book:ENGLISH SATChapter:LINEAR FUNCTIONS Exercise:EXERCISES
Explore 7 Videos
Similar Questions
Knowledge Check
In the standard (x,y) coordinate plane , point A is located at (w,w+5) and point B is located at (4w,w−5) . In coordinate units , what is the distance between A and B ?
A√9w2+2w+10B√9w2+100C9w2+100D|w|√11In the standard (x,y) coordinate plane, what is the slope of the line 3x+8y=5?
A−3B−38C35D3If 17x−5y=8and14x−7y=−7, what is the value of 3x+2y ?
A−15B−5C5D15
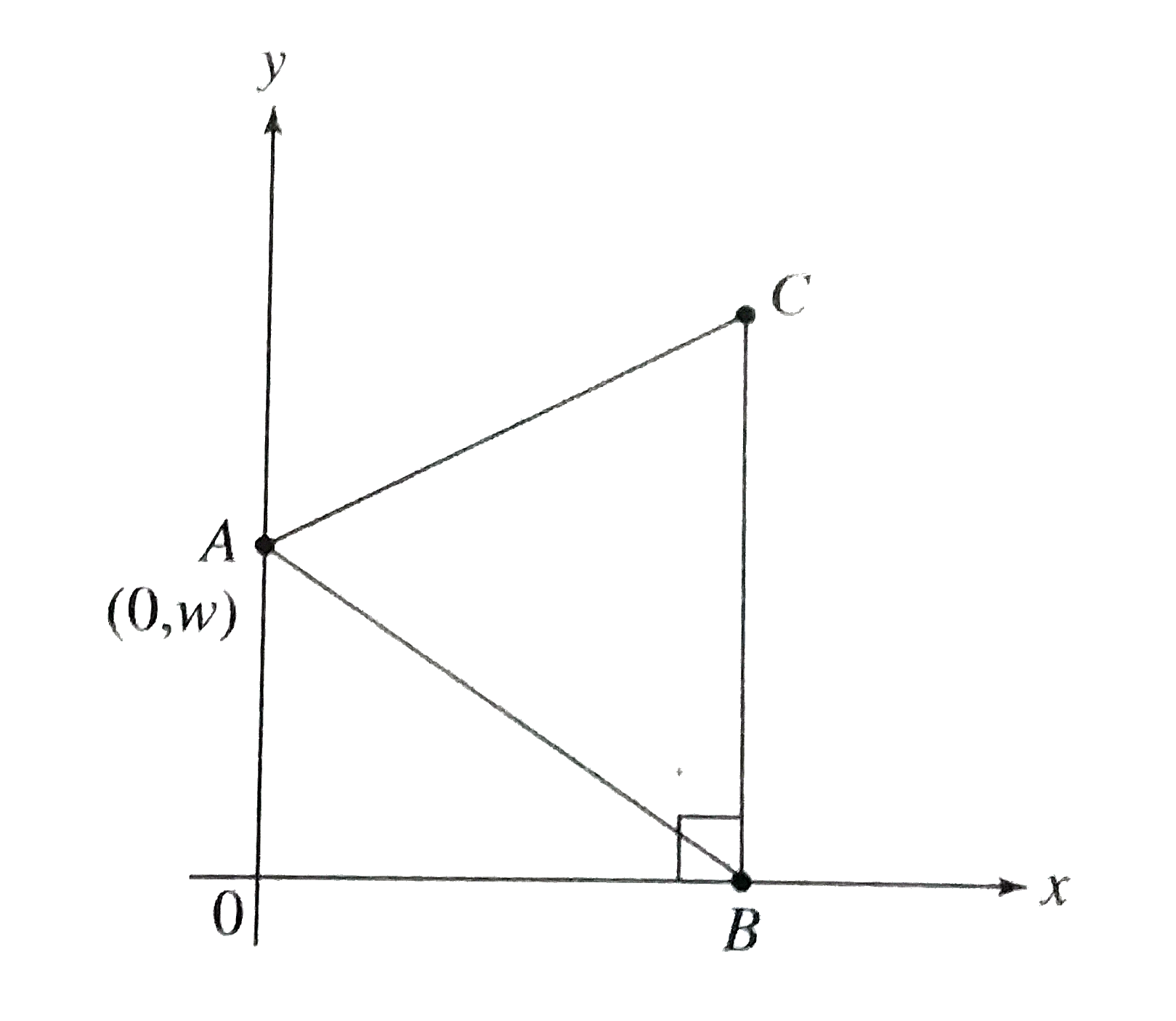
ΔABC , shown below in the standard (x,y) coordinate plane is equilateral with vertex A at (0,w) and vertex B on the x- axis as shown . What are the coordinates of vertex C ?
View SolutionWhen points A and B (-3, 4) are graphed in the standard (x,y) coordinate plane below, the midpoint of ¯¯¯¯¯¯AB will be (1,2). What will be the coordinate of point A?

View SolutionThe equation (x−7)2+(y−8)2=10 is that of a circle that lies in the standard (x,y) coordinate plane. One endpoint of a diameter of the circle has y-coordinate 11. What is the y-coordinate of the other endpoint of that diameter?
View SolutionIf 8x−2y=10and3y−9x=12, then what is the value of y−x ?
View SolutionIn the standard (x,y) coordinate plane, the circle centerd at (1,3) that passes through (4,7) is the set of all points that are:
View Solution

