If a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
Given D E | B C
In triangle A D E and A B C
∠DAE=∠BAC (common argle)
∠ADE=∠ABC[because D E | B C therefore correaponding anglas are equal ]
∠ABD=∠ACB
therefore triangleADEsimAABC
Hence ADAB=AEAC (in similar triangle, corresponcing sides are in szme ratio)
because ADAB=ABAC
=ABAD=ACAE
=ABAD−1=ACAE−1
=AB−ADAD=AC−ABAE
=DBAD=ECAE
=ADDB=ABBC
It is proved that if a line is drawn parallel to one side of a triangle intersecting the other two side, then it divides the two sides in the same ratio.
Topper's Solved these Questions
Similar Questions
Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
View SolutionTheorem 6.1 : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
View Solution
Knowledge Check
Thales theorem is given by a greek mathematician. According to this theorem, if a line is drawn parallel to one side of a triangle then it divides the other two sides in the same ratio. This theorem is also known as Basic Proportionality Theorem.
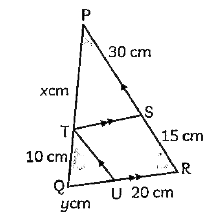
Here, the value of x is :A20 cmB15 cmC5 cmD10 cm
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Using the above result, do the following:
In Fig. 7 .45 DE||BC and BD = CE. Prove that ΔABC is an isosceles triangle.
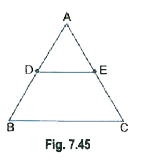
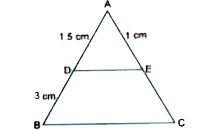
View SolutionIf a line is drawn parallel to one side of a triangle to intersect the other two sides in disinct points, the other two sides are divided in the same ratio. Using this theoure. Find EC in if DE∣∣BC.
View SolutionBasic proportionality Theorem or Thales Theorem - If a line is drawn parallel to one side of a triangle intersecting the other two sides; then it divides the two sides in the same ratio.
View SolutionProve that , "If a line parallel to a side of a triangle intersects the remaining sides in two distinct points then the line divides the sides in the same proportion".
View Solution(B) Solve any two of the following subquestions :
Prove that following statement, " If a line parallel to a side of a Delta intersects the remaining sides in two distinct points , then the line divides the sides in the same proportion . "
View SolutionIf a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral, so formed is cyclic.
View SolutionIf two sides of a cyclic quadrilateral are equal, prove that the other two sides are parallel.
View Solution
