There are two examination rooms A and B. If 10 candidates are sent A and B, the number of students in each room is same. If 20 candidates are sent from B to A, the number of students in A is double the number of students in B. Find the number of students in each room.
Let the no: of students in rooms A and B be x and y respectively.
Then, x-10=y+10
⇒{x}−{y}=20 →(1)
and {x}+20=2({y}-20)
⇒{x}−2{y}=−60{ (ii) }
Solving (1) and (ii) simultaneously,we get,
x=100 { } y=80
therefore The no: of students in room A is 100 in room B is 80 .
Related Playlists
Similar Questions
There are some students in the two examination halls A and B. To make the number of students equal in each hall, 10 students are sent from A to B but, if 20 students are sent from B to A, the number of students in A becomes double the number of students in B, then find the number of students in the both halls.
View SolutionThere are two class rooms A and B having a certain number of students. If 5 students are shifted from room A to room B, the resulting number of students in both the rooms becomes equal. If 5 students are shifted from room B to room A, the resulting number of students in room A becomes double the number of students left in room B. Find the original number of students in both the rooms separately.
View SolutionThere are two examination halls P and Q. If 10 students shifted P to Q, then the number of students will be equal in both the examination halls. If 20 students shifted from Q to P,then the students of P would be doubled to the students of Q. The numbers of students would be in P and Q, respectively are
View SolutionIn a school, the number of students in each section is equal to the number of sections. If the total number of students is 625, then find the numbr of sections
View SolutionThe pie chart given below shows the number of students in 6 different sections. The total number of students is 1800.
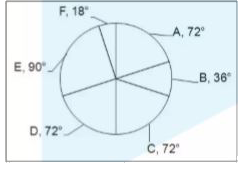
What is the ratio of number of students in section D to the number of students in section F and B?View SolutionOut of 30 students in a class, 20 like cricket and 10 like Hockey. The ratio of the number of students liking Hockey to the total number of students is
View SolutionThe pie chart given below shows the number of students in 5 sections .The number of students is 7200.
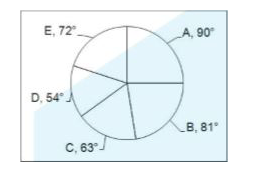
What is the total number of students in section E and section B?View SolutionThe sum of the number of male and female students in an institute is 100. If the number of male students is x, then the number of female students becomes x % of the total number of students. Find the number of male students.
View SolutionThere are 20 teachers in a school of 500 students. The ratio of the number of teachers to the number of students is
View SolutionThe pie chart given below shows the number of students in 5 sections .The number of students is 7200.
The number of students in section A is what percent of that of section B?
 View Solution
View Solution


